Основное свойство дроби - урок 2 - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: учить применять основное свойство дроби при выполнении заданий; развивать грамотную математическую речь; совершенствовать сочетание индивидуальной и коллективной форм работы с учащимися; проверить знания и навыки учащихся по изученному материалу.

Ход урока

I. Организационный момент

II. Устный счет

1. В Древнем Риме при измерении величин применялись дроби со знаменателем 12.

Вместо 1/12 говорили «одна унция», вместо 5/12 - «пять унций» и т. д. Выразите в унциях: половину, треть, четверть, пять шестых, три четверти. (Половина — 6 унции, треть — 4 унции, четверть — 3 унции, пять шестых — 10 унций, три четверти — 9 унций.)

2. Укажите среди данных произведений разложение числа 500 на простые множители: а) 25 · 2 · 10; б) 2 · 2 · 2 · 5 · 5 · 5; в) 4 · 5 · 5 · 5; г) 2 · 2 · 5 · 5 · 5.

3. Найдите наибольший общий делитель и наименьшее общее кратное чисел: а) 6 и 8; б) 12 и 20; в) 24 и 48; г) 5 и 7; д) 12 и 15; е) 1 и 50.

4. Задание на развитие памяти.

Посмотрите 15 сек надроби и попробуйте их запомнить: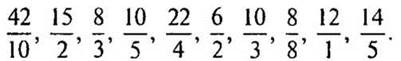

— Запишите в тетрадь, какие дроби вы запомнили.

— Проверьте.

— Если запомнили больше половины, то хорошо.

— Выделите целую часть из неправильных дробей, записанных на доске.

5. Замените каждую из следующих дробей дробью, знаменатель которой равен 20.

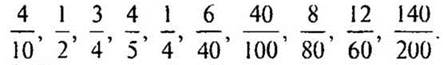
6. Заяц вытащил 8 морковок и съел их все, кроме 5. Сколько морковок осталось? (5.)

III. Индивидуальная работа

2 человека работают у доски по индивидуальным карточкам, в это время с остальными учащимися проводится устная работа. В конце работы всем учащимся предлагается проверить правильность выполнения заданий.

1 карточка

1. Найдите все делители числа и расположите их в порядке убывания: а) 40: б) 51; в) 17.

2. Разложите число на простые множители: а) 60; б) 500: в) 196.

2 карточка

1. Найдите все делители числа и расположите их в порядке убывания: а) 50: б) 21; в) 13.

2. Разложите число на простые множители: а) 80; б) 300; в) 135.

IV. Сообщение темы урока

— Сегодня мы будем учиться применять основное свойство дроби при выполнении различных заданий.

V. Закрепление изученного материала

1. № 213 стр. 36 (работа в парах).

(Во время обсуждения решения подойти к ребятам, послушать их ответы. Попросить более сильных учащихся, объяснить решения слабым ученикам. Отвечают слабые ученики).

2. Практическая работа.

№ 238 стр. 38 (на доске и в тетрадях).

(Ответ: координатами одной и той же точки являются числа: .)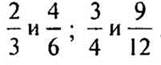

— Запишите соответствующие равенства: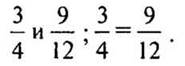

— Прочитайте равенство двух дробей разными способами. (Дробь две третьих равна дроби четыре шестых: дроби две третьих и четыре шестых равны; две третьих равны четырем шестым.)

3. № 237 стр. 38 (самостоятельно).

— Что можете сказать о получившихся дробях? (Равны.)

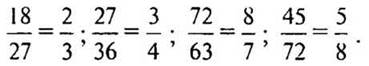
4. № 218 стр. 36 (устно).

— Что нужно сделать, чтобы ответить на вопрос задачи? (Сначала 12 разделить на знаменатель, затем числитель умножить на получившееся число.)

Решение:

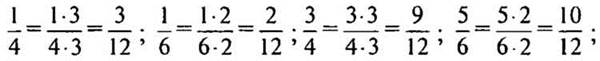
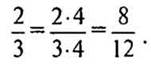
— Сколько двадцатичетвертых долей содержится в данных дробях?

Решение:

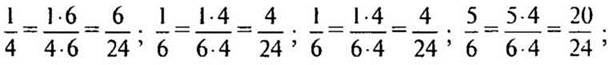
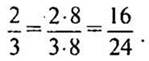
5. № 219 (устно).

— Назовите еще по три дроби, равные данным дробям.

6. Объясните, почему верны равенства:

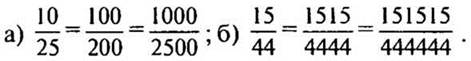
VI. Физкультминутка

VII. Работа над задачей

1. а) Выберите правильное утверждение:

A) Скорость — это расстояние между двумя точками.

Б) Скорость — это расстояние, пройденное телом за единицу времени.

B) Скорость — это быстрая езда.

б) Выберите правильное утверждение:

A) Чтобы найти расстояние, надо скорость разделить на время.

Б) Чтобы найти расстояние, надо время разделить на скорость.

B) Чтобы найти расстояние, надо скорость умножить на время.

2. № 233 (2) стр. 38 (после разбора самостоятельно).

— Прочитайте задачу.

— Как найти расстояние, зная скорость и время? (Чтобы найти расстояние, надо скорость умножить на время.)

— Как найти время, зная расстояние и скорость? (Чтобы найти время, надо расстояние разделить на скорость.)

Решение:

1) 5,2 · 4,5 = 23,4 (км) — прошли по дороге.

2) 32,4 - 23,4 = 9 (км) — осталось пройти.

3) 9 : 2,5 = 90 : 25 = 3,6 (ч) — шли по болотистой местности.

4) 4,5 + 1,6 + 3,6 = 9,7 (ч) — затрачено на весь поход.

(Ответ: 9,7 ч.)

3. № 232 стр. 37 (самостоятельно, устное обсуждение решения). Решение:

1) 12 · 11 · 10 · 9 = 132 · 90 = 11 880 (способами) - можно составить команду из 4 человек, но где встречаются перестановки из 4 человек.

2) 4 · 3 · 2 · 1 = 24 (перест.) - встречаются в данных способах.

3) 11 880 : 24 = 495 (способов) — можно составить команду из 4 человек.

4) 4 · 3 · 2 · 1 = 24 (сп.) - распределить этапы эстафеты.

(Ответ: 11 880 способами; 24 способами.)

VIII. Закрепление изученного материала

1. Между какими последовательными натуральными числами заключено число: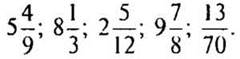

Ответ можно записать в виде неравенства или написать только два натуральных числа.

(Ответ: )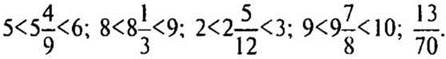

Последняя дробь больше нуля, но нуль не является натуральным числом, поэтому ответить на данный вопрос нельзя.

2. № 230 (б) стр. 37 (самостоятельная работа с последующей взаимопроверкой).

Решение:

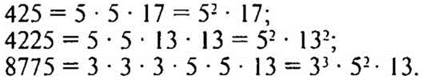
— Назовите простые числа, которые удовлетворяют неравенству 1 < а < 23.

(Первым трем ответившим ученикам можно поставить оценку.)

3. № 231 стр. 37 (у доски и в тетрадях).

Решение:

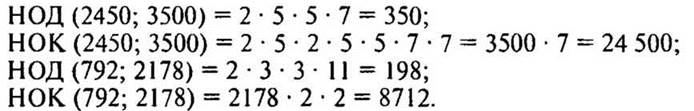
4. № 235 стр. 38.

— Как удобнее сосчитать?

— Какое свойство умножения использовали? (Распределительное.)

— Запишите его в буквенном виде.

Распределительный закон умножения относительно сложения:

Распределительный закон умножения относительно вычитания:

— Чтобы умножить число на 0,25, можно это число разделить на 4.

5. Найдите значение выражений:

Решение:

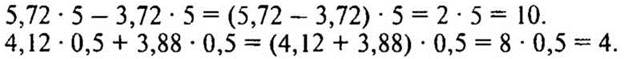
IX. Самостоятельная работа (10 мин)

Вариант I

1. Запишите две дроби, равные: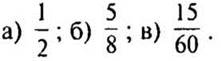

2. В равенстве вместо буквы запишите такое число, чтобы равенство было верным: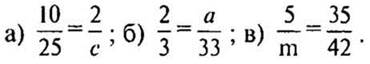

3. Сравните числа: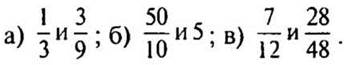

Вариант II

1. Запишите две дроби, равные: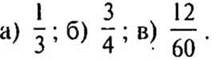

2. В равенстве вместо буквы запишите такое число, чтобы равенство было верным: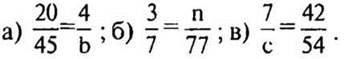

3. Сравните числа: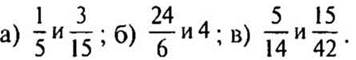

X. Подведение итогов урока

— В чем состоит основное свойство дроби?

— Назовите его для дробей: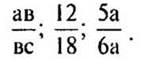

— Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3?

Домашнее задание: № 220, 221 (в, г) стр. 36; № 239 (б), 240 (б, г), 241 (б) стр. 38.

По желанию № 229 стр. 37.