Приведение дробей к общему знаменателю - урок 3 - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: повторить и закрепить изученный материал; отрабатывать навык приведения дробей к НОЗ; развивать умение решать комбинаторные задачи; проверить знания и навыки учащихся по изученному материалу.

Ход урока

I. Организационный момент

II. Устный счет

1. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 5 и 12; 12 и 18; 30 и 25; 9 и 4; 6 и 2; 4 и 24; 26 и 39; 50 и 20; 13 и 7.

2. Приведите дроби к наименьшему общему знаменателю: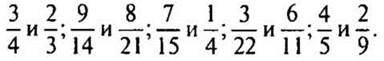

3. Бабушка поливает огород за 15 мин. Какую часть огорода она польет за 7 мин?

4. Если в 12 ч дня идет дождь, то можно ли утверждать, что через 36 ч будет солнечная погода? (Нет, потому что будет полночь.)

5. Двое отцов и двое сыновей застрелили трех зайцев, каждый — по одному. Как это получилось? (Это были дед, отец, сын.)

III. Индивидуальная работа

Два человека работают у доски по индивидуальным карточкам, в это время с остальными учащимися проводится устная работа.

1 карточка

1. Приведите дроби к НОЗ: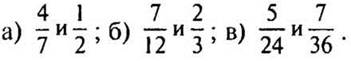

2. Выполните действия: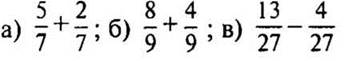

2 карточка

1. Приведите дроби к НОЗ: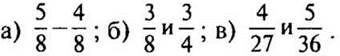

2. Выполните действия: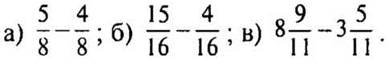

IV. Сообщение темы урока

— Сегодня на уроке мы рассмотрим более сложные случаи нахождения НОЗ дробей.

V. Изучение нового материала

1. Подготовительная работа.

— Найдите НОК чисел 72 и 99.

— Что для этого надо сделать? (Разложить числа на простые множители.)

2. Работа над новой темой.

— Найдите НОЗ дробей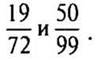

— Что нам в этом поможет? (Разложение на простые множители знаменателей.)

— Что является НОЗ дробей? (Так как наименьшим общим знаменателем является наименьшее общее кратное, то НОЗ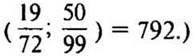

— Как найти дополнительный множитель? (Дополнительным множителем для дроби 19/72 является число 11, а для дроби 50/99 — произведение 2 · 2 · 2 = 8, то есть те множители, которые мы не подчеркнули.)

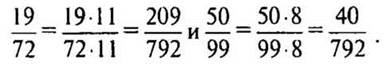
— Какой вывод можно сделать? (В более сложных случаях и дополнительные множители находят с помощью разложения на простые множители.)

VI. Физкультминутка

VII. Работа над задачей

№ 293 стр. 47 (у доски и в тетрадях с подробным комментированием).

Так как на первом месте могут стоять только 4 цифры (3, 5, 6, 8), на втором, третьем, четвертом — любая из пяти цифр, а на последнем, пятом, — только четные цифры, то есть только три (0, 6, 8), то по правилу произведения получаем: 4 · 5 · 5 · 5 · 3 = 1500 (чисел).

VIII. Закрепление изученного материала

1. № 283 (ж—м) стр. 46 (у доски и в тетрадях с подробным комментированием).

Решение:

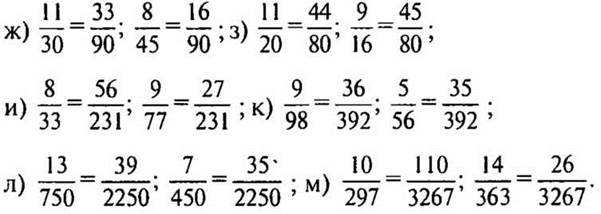
2. № 282 стр. 46 (один ученик на обратной стороне доски, остальные в тетрадях, самопроверка).

Решение:

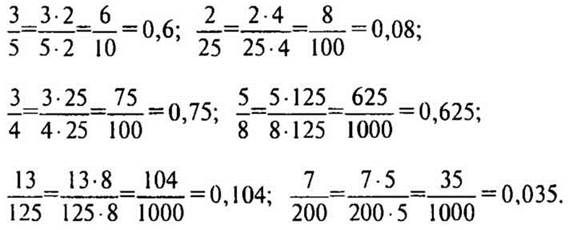
IX. Самостоятельная работа (10 мин)

Вариант I

1. Сократите дроби: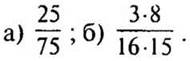

2. Приведите дробь 3/4 к знаменателю 20, а дробь 20/72 к знаменателю 18.

3. Приведите дроби к наименьшему общему знаменателю:

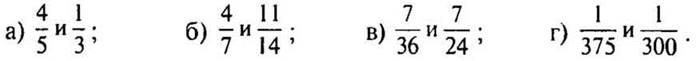
4. Приведите дроби к наименьшему общему знаменателю, предварительно сократив их: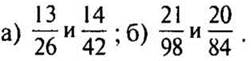

Вариант II

1. Сократите дроби: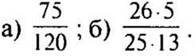

2. Приведите дробь 4/7 к знаменателю 28, а дробь 48/108 к знаменателю 9.

3. Приведите дроби к наименьшему общему знаменателю: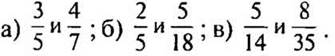

4. Приведите дроби к наименьшему общему знаменателю, предварительно сократив их: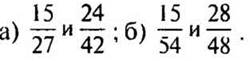

X. Закрепление изученного материала

1. Сократите дроби: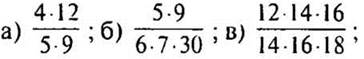

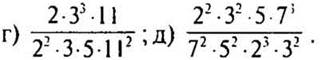
2. Какую часть метра составляет 1 см, 8 см. 40 см, 69 см, 90 см?

3. Какую часть килограмма составляет 2 г, 34 г, 50 г, 120 г, 324 г, 400 г, 650 г?

XI. Подведение итогов урока

— Наш урок подошел к концу. Скажите, что вам понравилось, а что нет?

— Какое задание вызвало наибольшее затруднение? (Выставляются оценки.)

Домашнее задание: № 298, 299, 300 (ж, з), 296 (1) стр. 48.