Сравнение дробей с разными знаменателями - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ - ОБЫКНОВЕННЫЕ ДРОБИ

Цели: поставить проблему по теме урока и найти выход из нее; вывести правила сравнения дробей с разными знаменателями; учить сравнивать дроби с разными знаменателями; продолжить формирование коммуникативных отношений.

Информация для учителя По ходу выполнения заданий в течение всех уроков учащиеся проговаривают правила сравнения, сокращения, сложения и вычитания обыкновенных дробей, формулируют основное свойство дроби.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний учащихся

1. Ознакомить учащихся с результатами самостоятельной работы.

2. Решить задания, где допущено наибольшее количество ошибок.

III. Устный счет

1. Назовите несколько чисел, которые имеют только три делителя. Какую закономерность можно заметить? (9, 25, 49, 81 — это квадраты натуральных чисел, сами числа являются нечетными.)

2. Сократите: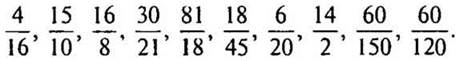

3. Приведите дроби к наименьшему общему знаменателю: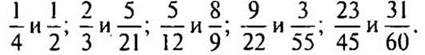

4. Учитель проверяет все тетради за 22 мин.

Какую часть тетрадей проверит учитель за 1 мин? за 9 мин? за 16 мин?

5. Полный ящик с фруктами весит 22 кг. Ящик, заполненный наполовину, весит 12 кг. Сколько весит пустой ящик?

Решение:

1) 22 - 12 = 10 (кг) — весит половина фруктов.

2) 12 - 10 = 2 (кг).

(Ответ: 2 кг весит пустой ящик.)

IV. Индивидуальная работа

1 карточка

1. Приведите дробь 2/3 к знаменателю 9, а дробь 32/40 к знаменателю 5.

2. Приведите дроби к наименьшему общему знаменателю:

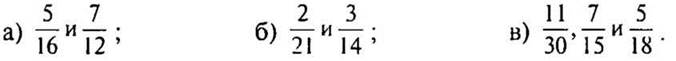
2 карточка

1. Приведите дробь 8/9 к знаменателю 18, а дробь 56/72 к знаменателю 9.

2. Приведите дроби к наименьшему общему знаменателю:

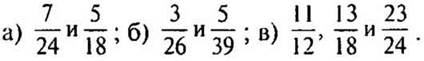
V. Сообщение темы урока

— Сегодня на уроке мы будем сравнивать дроби с разными знаменателями.

VI. Актуализация знаний учащихся

— А сейчас вспомним, как сравниваются дроби с одинаковыми знаменателями или с одинаковыми числителями.

1. Распределите числа по группам: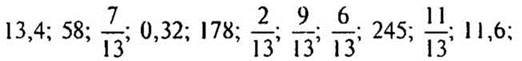

— По какому принципу вы распределили числа?

(Ответ: на 2 группы:

целые числа: 58; 178; 245;

дробные числа: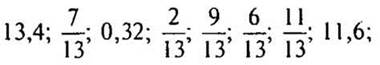

на 3 группы:

целые числа: 58; 178; 245;

обыкновенные дроби: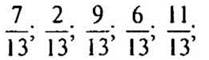

десятичные дроби: 13,4; 0,32; 11,6.)

— Расположите данные дроби в порядке возрастания.

— А как вы узнали, что дроби надо было так расположить?

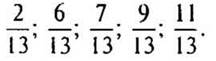
(Ответ: 2/13 — самая маленькая дробь, 11/13 — самая большая дробь).

— Какое правило сравнения дробей использовали? (Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

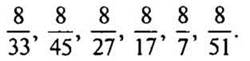
2. Запишите дроби в порядке убывания:

— Что значит записать дроби в порядке убывания? (От наибольшего числа к наименьшему числу.)

— Как сравнивать дроби с одинаковыми числителями? (Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.)

Решение:

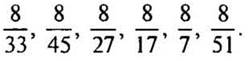
VII. Изучение нового материала

1. Подготовительная работа.

— А теперь предлагаю вам сравнить дроби. Рассмотрите их.

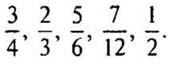
— Что вы заметили? (Знаменатели и числители у дробей разные.)

— Найдите среди этих дробей самую маленькую и самую большую.

— Появилось много мнений. У нас возникла проблема: как сравнить дроби с разными знаменателями?

— Чтобы ответить на вопрос, мы проведем исследовательскую работу. Работать будем в группах по инструкции.

(Инструкцию записать на доске.)

Инструкция:

1. Внимательно рассмотрите числа.

2. Расположите эти дроби на координатном луче, самостоятельно выберите единичный отрезок.

3. Сравните полученные отрезки. Сделайте вывод.

4. Расположите дроби в порядке возрастания. Выделите наименьшую дробь зеленным цветом, а наибольшую - красным.

5. Постарайтесь сформулировать вывод: как сравнить дроби с разными знаменателями.

— Скажите, удобно ли каждый раз, сравнивая дроби, отмечать их на координатном луче?

— Как же сравнивать такие дроби?

— Сформулируйте правило сравнения дробей с разными знаменателями и числителями.

2. Работа над новой темой.

— Сравните дроби 2/3 и 3/5.

— Приведем дроби к наименьшему общему знаменателю. (Так как 3 и 5 взаимно простые числа, то НОЗ дробей будет их произведение.)

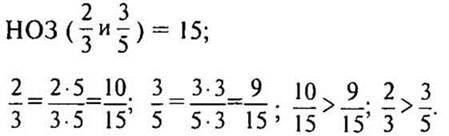
3. Учебник, стр. 50 (в некоторых учебниках опечатка — вместо слова «дательном» должно быть написано «родительном»).

— Прочитайте текст под рубрикой «Говори правильно».

— Прочитайте двумя способами данные записи: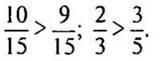

(Десять пятнадцатых больше девяти пятнадцатых или дробь десять пятнадцатых больше дроби девять пятнадцатых.)

VIII. Физкультминутка

IX. Закрепление изученного материала

1. № 304 (а, б) стр. 50 (у доски объясняет сильный ученик, остальные — в тетрадях).

— Как сравнивать дроби с разными знаменателями?

Решение:

а) Сравним дроби 2/3 и 8/21.

— Приведем дроби к наименьшему общему знаменателю. (Так как 21 делится на 3, то НОЗ дробей будет больший знаменатель 21.)

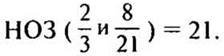
— Как сравнивать дроби с одинаковыми знаменателями? (Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

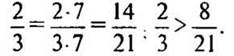
б) Сравним дроби 4/15 и 2/5.

— Приведем дроби к наименьшему общему знаменателю. (Так как 15 делится на 5, то НОЗ дробей будет больший знаменатель 15.)

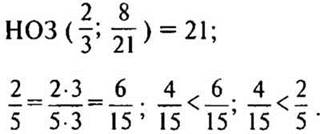
2. № 305 стр. 50 (решение записывать короче, все объяснение проговаривать).

Решение:

(Ответ: а) 1/30; б) 9/14.)

X. Самостоятельная работа

Взаимопроверка. Ответы на доске.

Вариант I. № 311 (а, б) стр. 51, № 352 (а) стр. 56.

Вариант II. № 311 (в, г) стр. 51, № 352 (б) стр. 56.

XI. Работа над задачей

I. № 313 стр. 51 (у доски и в тетрадях).

— Прочитайте задачу.

— Что нужно сделать, чтобы ответить на вопрос задачи? (Сравнить дроби.)

Решение:

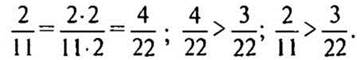
(Ответ: рисунки занимают больше места в книге.)

2. № 315 стр. 51 (у доски и в тетрадях).

— Что известно в задаче?

— Что надо узнать?

— Что примем за единицу? (Всю работу.)

Решение:

Пусть 1 — вся работа.

Какую часть бассейна заполняет узкая труба за 1 ч? 1/10 (часть).

Какую часть бассейна заполняет широкая труба за 1 ч? 1/4 (часть).

Какую часть бассейна заполняет узкая труба за 7 ч? 7/10 (бассейна).

Какую часть бассейна заполняет широкая труба за 3 ч? 3/4 (бассейна).

Какая труба дает меньше воды?

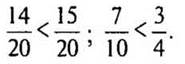
(Ответ: узкая труба.)

3. № 355 стр. 56 (после разбора самостоятельно).

— К какому виду задач можно отнести данную задачу? (К комбинаторным.)

— Первым уроком какой урок может быть? (Любой из пяти.)

— Вторым уроком какой урок может быть? (Любой из оставшихся четырех.)

— Третьим уроком какой урок может быть? (Любой из оставшихся трех.)

— Четвертым уроком какой урок может быть? (Любой из оставшихся двух.)

— Пятым уроком какой урок может быть? (Только какой-то один урок.)

— Какое правило будем использовать при решении задачи? (Правило произведения.)

Решение:

5 · 4 · 3 · 2 · 1 = 120 (вариантов).

(Ответ: 120 вариантов.)

XII. Повторение изученного материала

№ 281 (б) стр. 46 (устно с подробным комментированием).

Решение:

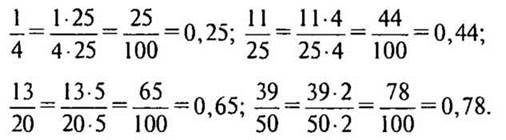
XIII. Подведение итогов урока

— Как сравнивать дроби с одинаковыми знаменателями?

— Как сравнивать дроби с одинаковыми числителями?

— Как сравнивать дроби с разными знаменателями?

Домашнее задание

Учебник, стр. 50 (прочитать текст под рубрикой «Говори правильно»). № 359 (а-г), 361 стр. 57; № 370 стр. 58.