Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Неравенство треугольника
Каждому из опыта известно, что самый короткий путь между точками на плоскости идет по прямой. Оказывается, что это можно доказать, исходя из уже пройденных раньше аксиом. Ключом к данному доказательству служит так называемое
Неравенство треугольника. Сумма любых двух сторон в треугольнике всегда больше его третьей стороны.
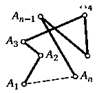
Неравенство ломаной. Длина ломаной не может быть меньше длины отрезка, соединяющего ее начало и конец. Равенство возможно только в случае, когда все вершины ломаной лежат на данном отрезке.
1. Используя данный чертеж, докажите неравенство треугольника.
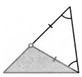
2. Докажите «неравенство трех точек»: для любых трех точек А, В, С на плоскости АВ + ВО АС. В каком случае будет равенство?
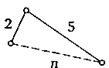
3. Две стороны треугольника равны 2 и 5, а третья равна целому числу. Каким оно может быть?
4. Одна сторона равнобедренного треугольника равна 5, а другая 12. Найдите периметр треугольника.
5. Одна сторона треугольника равна 4, а длины двух других его сторон относятся как 3:5. Докажите, что периметр треугольника меньше 20.
6. Разность боковых сторон треугольника равна 2, а его основание в три раза больше меньшей из них. Докажите, что периметр треугольника больше 5.
7. Внутри треугольника взяли произвольную точку. Докажите, что сумма расстояний от нее до вершин треугольника больше половины его периметра.
8. Отрезки АС и BD пересекаются. Докажите, что AB + CD < <="" p="">
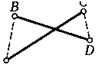
А
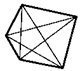
9. Докажите, что сумма длин всех диагоналей выпуклого пятиугольника больше его периметра.
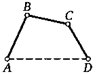
10. Докажите, что для произвольных точек А, В, С, D на плоскости АВ 4- ВС 4- CD > AD. В каком случае будет равенство?
11. Докажите неравенство ломаной.
12. Три стороны четырехугольника последовательно равны 1, 5 и 2. Какие значения может принимать длина его четвертой стороны, если известно, что она является целым числом?
13. На сторонах многоугольника взяли две точки. Докажите, что соединяющий их отрезок меньше половины его периметра. Останется ли верным утверждение задачи, если соединить две любые точки внутри многоугольника?
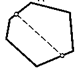
14. Докажите, что сумма диагоналей любого четырехугольника меньше его периметра.
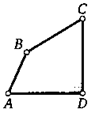
15. В четырехугольнике ABCD угол D прямой. Докажите, что CDKAB + BC.
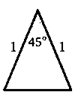
16. Боковые стороны равнобедренного треугольника равны 1, а угол между ними равен 45°. Докажите, что основание треугольника больше 1/2.
17. (Неравенство медианы.) Докажите, что медиана треугольника меньше полусуммы двух его сторон, выходящих из той же вершины.

18. Докажите, что отрезок, соединяющий середины противоположных сторон выпуклого четырехугольника, меньше полусуммы его диагоналей.

19. (Неравенство «резинки».) В треугольнике АВС взята произвольная точка О. Докажите, что АВ 4- ВС > АО 4- ОС.
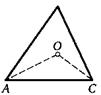
20. В треугольнике АВС взята произвольная точка О. Докажите, что АО 4- ВО 4- СО меньше периметра треугольника.
21. В треугольнике АВС взяли произвольные точки О и М. Докажите, что AM 4- ВЫ 4- СМ 4- ОМ > АО 4- ВО 4- СО.

22. Дан выпуклый четырехугольник. Где необходимо взять точку, чтобы сумма расстояний от нее до вершин четырехугольника была как можно меньше?
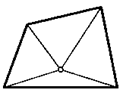
*23. Докажите, что аналогичная точка для невыпуклого четырехугольника совпадает с одной из его вершин.
24. Докажите, что точка с минимальной суммой расстояний до вершин многоугольника может быть только одна.
25. Один треугольник находится внутри другого. Докажите, что его периметр меньше.

26. Выведите из утверждения предыдущей задачи «правило веревки».
27. Как из бумажного треугольника вырезать четырехугольник с большим периметром?
28. Все стороны четырехугольника равны. Внутри него взяли произвольную точку. Докажите, что сумма расстояний от этой точки до вершин четырехугольника меньше его периметра.
29. Может ли сумма расстояний от некоторой точки внутри выпуклого четырехугольника до его вершин быть больше периметра четырехугольника?