Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Параллельность. Сумма углов треугольника
Прямые называются параллельными, если они не пересекаются.
только одна М
Аксиома параллельных (пятый постулат Евклида). Через точку, не лежащую на прямой, можно провести не более одной прямой, параллельной данной.
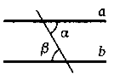
если а = Р, то а \\Ъ если а || Ь, то а = Р
Признак параллельных (теорема). Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то прямые параллельны.
Свойство параллельных (обратная теорема).
Если прямые параллельны, то любая секущая их прямая образует с ними равные накрест лежащие углы.
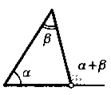
Теорема об углах треугольника. Сумма углов любого треугольника равна 180°.
Вторая теорема о внешнем угле. Внешний угол треугольника равен сумме двух не смежных с ним внутренних его углов.
Теорема о сумме углов многоугольника.
Сумма внутренних углов п-угольника равна 180° • (п —2).
1. (Транзитивность параллельности.) Докажите, что две прямые, параллельные третьей, параллельны между собой.
2. Прямая пересекает одну из параллельных прямых. Докажите, что она пересечет и другую.
3. К двум сторонам треугольника провели перпендикуляры. Докажите, что они пересекаются.
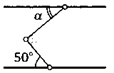
4. Сторона прямого угла образует с одной из параллельных прямых угол в 50°. Какой угол образует вторая сторона этого угла с другой параллельной прямой?
5. Две пары параллельных прямых образуют четырехугольник. Докажите, что его противоположные углы равны.
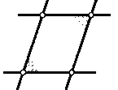
6. Противоположные стороны четырехугольника попарно равны. Докажите, что они лежат на двух парах параллельных прямых.
7. Один угол равнобедренного треугольника в два раза больше другого. Найдите углы треугольника.
8. Биссектриса угла при основании равнобедренного треугольника образует с противоположной стороной угол 75°. Определите угол при основании треугольника.
9. Один угол шестиугольника прямой, а все другие равны между собой. Найдите величину этих углов.

10. При каждой вершине выпуклого многоугольника отметили один внешний угол. Найдите сумму всех таких углов.

11. Середина стороны треугольника равноудалена от всех его вершин. Докажите, что этот треугольник прямоугольный.
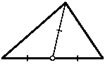
12. Биссектрисы углов Л и С треугольника АВС пересекаются в точке О. Угол АВС равен а. Найдите угол АОС.
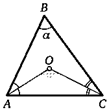
13. Угол между высотой и биссектрисой, проведенными из одного угла треугольника, равен а. Найдите разность двух других его углов.
14. На стороне квадрата внутрь его построили равносторонний треугольник. Найдите угол а на чертеже.
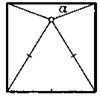
К задаче 14
В С
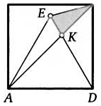
15. На стороне квадрата ABCD построили равносторонний треугольник AED. Диагональ АС пересекает его сторону ED в точке К. Верно ли, что треугольник СЕК равнобедренный?
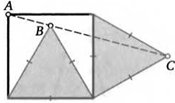
16. На двух сторонах квадрата построены равносторонние треугольники. Лежат ли отмеченные на рисунке точки Л, В и С на одной прямой?
17. Луч света последовательно отражается от двух взаимно перпендикулярных зеркал. Докажите, что он «возвращается» по параллельному направлению. (Считается известным, что угол падения луча света на зеркало равен углу его отражения.)

Замечание: на этом принципе основана работа катафота или уголкового отражателя: если размеры одного «уголка» зеркальной «лесенки» малы, то катафот возвращает световой луч приблизительно туда, откуда он пришел.
18. Чему равна сумма углов при вершинах произвольной пятиконечной звезды?

19. Тот же вопрос для такой семиугольной замкнутой ломаной, которая показана на рисунке. (см. рисунок). Найдите разность двух других углов треугольника.

20. Два угла расположены так, что их стороны взаимно перпендикулярны. Докажите, что а) величины этих углов равны; б) их биссектрисы перпендикулярны друг другу.
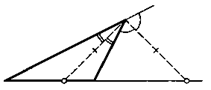
21. Биссектриса одного угла треугольника равна биссектрисе его внешнего угла при той же вершине (см. рисунок). Найдите разность двух других углов треугольника.
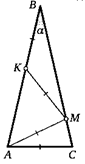
22. На боковых сторонах АВ и ВС равнобедренного треугольника АВС взяли точки М и К соответственно так, что ВК = КМ = = АМ = АС. Найдите угол треугольника, противоположный основанию.
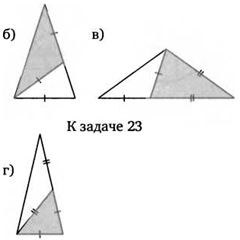
23. Равнобедренный треугольник таков, что его можно разрезать на два меньших равнобедренных треугольника. На рисунках показано, как это можно сделать. Найдите углы при основаниях этих треугольников на рисунках.
24. На сторонах угла, равного а, взяли четыре точки А, В, С и D так, что отрезки АВ, ВС и CD равны (см. рисунок). Найдите угол между прямыми АС и BD.
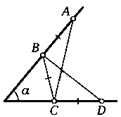
В
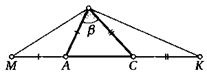
25. На продолжении стороны АС треугольника АВС отложены точки М и К так, что AM = АВ, СК = ВС (см. рисунок). Найдите угол МВК, если угол АВС = /3.
26. Выпуклый шестиугольник таков, что его противоположные углы попарно равны. Докажите, что противоположные стороны такого шестиугольника параллельны.

*27. На рисунке изображены выпуклые семиугольник и девятиугольник, которые можно разрезать на квадраты и правильные треугольники. Существуют ли обладающие тем же свойством выпуклые а) 10-угольник; б) 12-угольник; в) 13-угольник?

28. В чем ошибка такого «доказательства» пятого постулата: Докажем, что через точку С проходит единственная прямая, параллельная АВ. Как известно, из точки С можно опустить единственный перпендикуляр CD на АВ. К прямой CD можно восстановить единственный перпендикуляр СЕ. Прямая СЕ параллельна АВ. Поскольку наши построения выполнены единственно возможным образом, такая прямая только одна.
![]()
D В
Л