Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Знакомство с окружностью

Хордой называется отрезок, соединяющий любые две точки окружности1.
Диаметром окружности называется хорда, проходящая через ее центр2.
1. Найдите ошибку в следующем определении окружности: «окружность — это множество точек плоскости, равноудаленных от данной точки».

2. Принадлежит ли окружности ее центр? Тот же вопрос для круга.
3. Докажите, что любая хорда окружности не превосходит ее диаметра.
4. Даны окружность и точка А, не лежащая на ней. Где на окружности необходимо взять точку В так, чтобы отрезок АВ был
а) самым коротким? б) самым длинным?
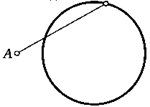
5. Прямая не пересекает окружность. Где на окружности находится точка, расстояние от которой до этой прямой наименьшее?
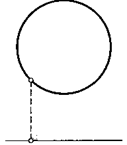
6. В окружности проведены две параллельные хорды. Докажите, что у них есть общий серединный перпендикуляр.
7. Докажите, что общая хорда двух пересекающихся окружностей перпендикулярна линии их центров.
8. Докажите, что равные хорды окружности находятся на одинаковых расстояниях от центра.
9. Хорда окружности делится пополам ее диаметром. Докажите, что либо эта хорда перпендикулярна данному диаметру, либо она сама проходит через центр окружности.
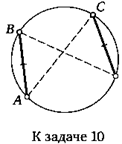
12. Хорды АВ и CD окружности равны (см. рисунок). Докажите, что прямые ВС и AD параллельны.
13. В окружность радиуса 1 вписан шестиугольник, все стороны которого равны. Найдите его периметр.
14. Как одним циркулем без линейки получить отрезок в два раза длиннее данного? А в три раза длиннее?
15. (Свойство диаметра окружности.) Докажите, что диаметр окружности из любой ее точки «виден» под прямым углом.
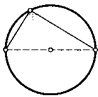
16. (Теорема.) Докажите, что медиана прямоугольного треугольника, проведенная к его гипотенузе, равна половине гипотенузы.

17. Два противоположных угла четырехугольника прямые. Докажите, что все его вершины лежат на одной окружности.
18. Два противоположных угла четырехугольника прямые, а его диагонали перпендикулярны. Докажите, что одна из них делит другую пополам.
19. На окружности отметили три точки. Как по ним найти ее центр?
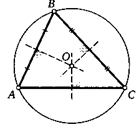
20. (Теорема об описанной окружности треугольника.) Докажите, что вокруг любого треугольника всегда можно описать только одну окружность. Центр этой окружности находится на пересечении серединных перпендикуляров ко всем сторонам данного треугольника.
21. Приведите пример четырехугольника, вокруг которого нельзя описать окружность.
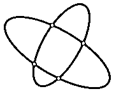
22. Как видно из рисунка, два овала могут пересекаться в четырех точках. А сколько общих точек могут иметь две окружности и почему?
23. Почему окружность и прямая не могут пересекаться более чем в двух точках?
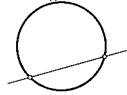
24. Две хорды окружности делят друг друга пополам. Докажите, что точка их пересечения — центр окружности.
25. Точки А, В, С, D в данном порядке лежат на одной окружности. На плоскости взяли такую точку М, что a) AM = DM, ВМ = СМ;
б) AM = СМ, ВМ = DM. Обязательно ли точка М находится в центре окружности?
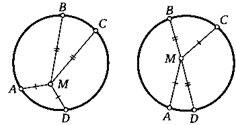
26. Центр описанной окружности лежит внутри треугольника. Докажите, что этот треугольник остроугольный.
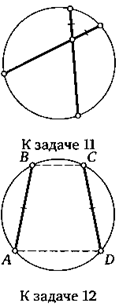
27. В окружность вписана простая ломаная, состоящая из трех равных звеньев. Расстояние между началом и концом ломаной равно радиусу окружности. Найдите угол между соседними звеньями ломаной. Внимание: у задачи два ответа!

28. Какой ответ будет в предыдущей задаче, если ломаная имеет самопересечения?
*29. Сколько существует замкнутых ломаных, вписанных в одну окружность, состоящих из семи равных звеньев и выходящих из точки М этой окружности?
30. В окружность вписана замкнутая пятизвенная ломаная, четыре звена которой равны, а пятое является диаметром окружности. Найдите угол между ее равными звеньями.
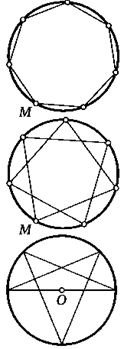
К задаче 29? 30