Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Построения циркулем и линейкой
С помощью линейки можно провести прямую через любые две точки плоскости.
С помощью циркуля можно провести окружность с центром в данной точке и радиусом, равным любому данному отрезку.
При дальнейших построениях можно пользоваться точками пересечения уже проведенных прямых и окружностей. Каким-либо другим способом использовать линейку и циркуль не разрешается.
Более сложные построения можно описывать в виде алгоритма, ссылаясь на элементарные построения.
Элементарные построения
1. Даны отрезок и луч. От начала луча отложите отрезок, равный данному.
2. Дан отрезок. Постройте к нему серединный перпендикуляр.
3. Даны прямая и точка, не лежащая на ней. Опустите из данной точки перпендикуляр на данную прямую.
4. Точка лежит на прямой. Восстановите перпендикуляр к прямой в данной точке.
5. Даны прямая и точка, не лежащая на ней. Проведите через эту точку прямую, параллельную данной.
6. Постройте биссектрису данного угла.
7. Постройте треугольник, стороны которого равнялись бы трем данным отрезкам. Когда это возможно?
8. От данного луча в заданную полуплоскость отложите угол, равный данному.
Задачи
9. Постройте угол 60°.
10. Постойте углы 30° и 105°.
11. Дан отрезок длины 1. Постройте отрезок длины 0,25.
12. Постройте четырехугольник, стороны которого равны 3 см, 4 см, 5 см и 6 см. Сколько можно построить таких четырехугольников?
13. Постройте прямоугольный треугольник по длинам его гипотенузы и одного из катетов.
14. Постройте треугольник по длинам двух его сторон и углу, лежащему против одной из них. Сколько решений может иметь задача?
15. Точка М находится внутри угла с вершиной О. Проведите через данную точку прямую, пересекающую стороны угла в таких точках Л и Б, что ОА = ОБ.
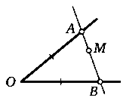
16. Даны прямая и точка М, не лежащая на ней. Постройте на данной прямой точку К так, чтобы отрезок МК образовывал с ней угол 30°.

17. Дана окружность. Постройте ее центр.
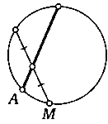
18. Точка М лежит внутри круга. Проведите через нее хорду так, чтобы точка М делила ее пополам.
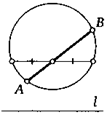
19. Даны окружность, хорда АВ этой окружности и прямая Z. Постройте хорду этой окружности, параллельную данной прямой, так, чтобы она делилась хордой АВ пополам.
20. Впишите в окружность равносторонний треугольник, одна вершина которого находилась бы в данной ее точке.
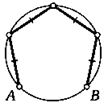
21. На окружности даны точки А и В. Впишите в данную окружность простую ломаную с концами в данных точках, состоящую из четырех равных звеньев.
В
22. Даны прямая и точки А и В. Постройте на прямой точку М так, что LAMB = 90°.
23. Даны окружность, хорда АВ и точка М на окружности. Проведите через данную точку еще одну хорду так, чтобы она делилась первой хордой пополам. В каком случае у задачи будет два решения?
24. Постройте прямоугольный треугольник по длинам его гипотенузы и высоты, опущенной на гипотенузу.
25. Постройте прямоугольный треугольник по гипотенузе и сумме его катетов.
26. Постройте треугольник по стороне, прилежащему к ней углу и отрезку, равному сумме двух других его сторон.
27. Постройте треугольник по стороне, прилежащему к ней углу и отрезку, равному разности двух других сторон.
28. Постройте треугольник по двум его сторонам и медиане, проведенной к третьей.
29. Постройте треугольник по медиане и двум углам, которые она образует со сторонами, выходящими с ней из одной точки.
30. Постройте треугольник по стороне, противоположному углу и сумме двух других его сторон.
*31. Постройте треугольник по двум его сторонам и разности противоположных от этих сторон углов.
*32. Постройте треугольник по двум его углам и периметру. .