Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Центральная симметрия

центральная симметрия Z0
Точки А и Аг называются симметричными относительно точки О, если О является серединой отрезка ААг. Если мы каждой точке А на плоскости поставим в соответствие симметричную ей точку Аъ то это значит, что на плоскости мы задали центральную симметрию. Точка О называется центром симметрии,, при симметрии она переходит сама в себя.
Центральная симметрия обозначается так: Z0.
Фигура называется центрально-симметричной, если при симметрии относительно некоторой точки она переходит сама в себя.
1. С помощью циркуля и линейки постройте точку, симметричную данной точке А относительно точки О. Можно ли это сделать только одним циркулем?
2. Докажите, что окружность имеет центр симметрии.
3. Имеют ли центр симметрии отрезок, луч, прямая?
4. Напишите три двузначных числа, десятичная запись которых имеет центр симметрии. Существуют ли такие трехзначные числа?
5. Какие буквы латинского алфавита имеют центр симметрии?
ABCDEFGHIJKLMNOPQRSTUVWXYZ
6. Какие координаты имеет точка, симметричная точке А(х; у) относительно начала координат?
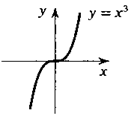
7. На рисунке показан график функции, заданной уравнением у = х3. Докажите, что он имеет центр симметрии.
8. Двое игроков по очереди кладут одинаковые монеты на круглый стол. Касаться уже лежащих монет или сдвигать их нельзя. Проигрывает тот, кто не может положить монету (так, чтобы она не упала со стола). Кто из игроков выиграет при правильной игре и как ему следует играть?
9. Докажите, что центральная симметрия не меняет расстояний: если точки Аг и Вг симметричны точкам АиВ относительно точки О, то расстояния Л1Б1 и АВ равны.
Л
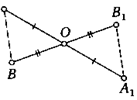
10. Докажите, что при центральной симметрии отрезок переходит в отрезок.
11. Докажите, что при центральной симметрии прямая переходит либо в параллельную ей прямую, либо сама в себя.
12. Точка не лежит на прямой. Постройте прямую, симметричную данной прямой относительно данной точки.
13. Докажите, что при центральной симметрии окружность переходит в окружность.
14. Верно ли, что центральная симметрия сохраняет величины углов?
15. Два равных отрезка лежат на параллельных прямых. Докажите, что существует центральная симметрия, переводящая один из них в другой.
16. Противоположные стороны шестиугольника попарно параллельны и равны. Докажите, что этот шестиугольник имеет центр симметрии.
17. Нарисуйте: а) четырехугольник; б) восьмиугольник, имеющие центр симметрии.
18. Может ли иметь центр симметрии пятиугольник?
19. Докажите, что любой эллипс имеет центр симметрии. Где находится ее центр?
20. Через данную точку М проведите прямую так, чтобы ее отрезок с концами на данной прямой и данной окружности делился точкой М пополам.
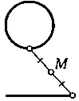
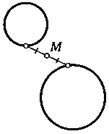
21. Через данную точку М проведите прямую так, чтобы ее отрезок на двух данных окружностях делился точкой М пополам.
22. Внутри треугольника взяли произвольную точку. Всегда ли можно провести через нее три прямые так, чтобы отрезок каждой из них внутри треугольника делился данной точкой пополам?
23. На круглый ломоть хлеба произвольно положили квадратный ломтик сыра. Как разрезать полученный бутерброд на две части, чтобы в них было поровну и хлеба, и сыра?

24. Некоторая фигура имеет две перпендикулярные друг другу оси симметрии. Докажите, что она имеет центр симметрии.
*25. Фирма «Оригинальный кафель» выпускает плитки для пола в форме четырехугольников без равных и параллельных сторон. Докажите, что при определенном умении такими плитками можно замостить всю плоскость.
