Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Параллелограммы
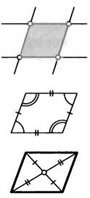
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны1.
Свойства параллелограмма
1. Противоположные углы параллелограмма равны.
2. Противоположные стороны параллелограмма равны.
3. Диагонали параллелограмма пересекаются и делят друг друга пополам точкой пересечения.
Признаки параллелограмма
1. Если в четырехугольнике противоположные углы попарно равны, то он — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то он — параллелограмм.
3. Если диагонали четырехугольника точкой пересечения делят друг друга пополам, то этот четырехугольник — параллелограмм.
4. Если у четырехугольника две стороны параллельны и равны одновременно, то он — параллелограмм.
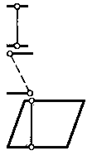
Расстоянием между параллельными прямыми называется длина отрезка общего перпендикуляра к этим прямым. Расстояние между параллельными прямыми не зависит от того, в какой точке проводится данный перпендикуляр и является наименьшим возможным отрезком, соединяющим точки этих прямых.
Высотой параллелограмма называется отрезок, перпендикулярный двум его противоположным сторонам (или их продолжениям).
1. Докажите первый признак параллелограмма.
2. Две стороны четырехугольника параллельны, а одна его диагональ делит другую пополам. Докажите, что данный четырехугольник — параллелограмм.
3. Через каждую вершину треугольника АВС параллельно его противоположной стороне провели прямую. Эти прямые образовали новый треугольник. Докажите, что вершины старого треугольника являются серединами сторон нового.
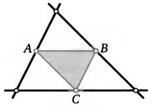
4. На двух сторонах параллелограмма построили равносторонние треугольники так, как показано на рисунке. Докажите, что треугольник АВС равносторонний.
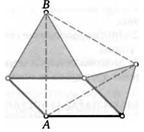
5. Докажите, что биссектриса угла, смежного с углом параллелограмма, перпендикулярна биссектрисе его противоположного угла.
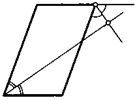
6. Биссектрисы двух углов при одной стороне параллелограмма делят другую его сторону на три равные части. Найдите отношение сторон параллелограмма.
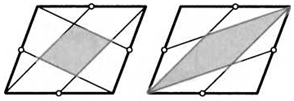
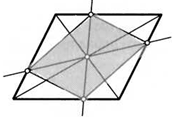
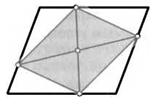
7. Вершины параллелограмма соединили с серединами его сторон так, как показано на рисунках. Докажите, что заштрихованные фигуры тоже параллелограммы.
8. Диагональ параллелограмма разбили на три равные части. Докажите, что полученные точки деления и две другие его вершины образуют новый параллелограмм.
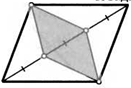
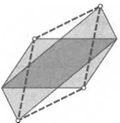
9. Из трех параллелограммов составили шестиугольник так, как это показано на рисунке. Докажите, что этот шестиугольник можно разбить на три параллелограмма другим способом.

10. На клетчатой бумаге отметили точки А, В, С так, как это показано на рисунке. Где необходимо взять четвертую точку D, чтобы получился параллелограмм ABCD?
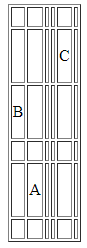
11. Прямая, параллельная стороне АС треугольника АВС, пересекает две другие стороны в точках М и К. Докажите, что МК < АС.
В
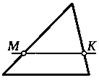
А
С
К задаче 11, к задаче 12
12. (Теорема о расстоянии между параллельными прямыми.) Докажите, что расстояние от всех точек одной прямой до параллельной ей прямой постоянно.
13. Три точки лежат по одну сторону от данной прямой и находятся на одинаковых расстояниях от нее. Докажите, что данные три точки лежат на одной прямой.
14. а) Где находятся все точки плоскости, расстояние от которых до некоторой прямой одинаково?
б) Где находятся все точки плоскости, равноудаленные от двух данных параллельных прямых?
15. На основании равнобедренного треугольника взята произвольная точка. Докажите, что сумма расстояний от нее до боковых сторон треугольника постоянна.

16. Через точку пересечения диагоналей параллелограмма провели две произвольные прямые. Докажите, что точки их пересечения с его сторонами образуют новый параллелограмм.
17. Две пары противоположных сторон шестиугольника соответственно параллельны и равны. Докажите, что третья пара его противоположных сторон обладает тем же свойством.
18. У двух параллелограммов совпадает пара противоположных вершин. Докажите, что остальные четыре их вершины образуют новый параллелограмм.
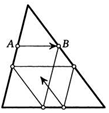
19. Из произвольной точки А, взятой на стороне треугольника, проводится прямая, параллельная другой его стороне и пересекающая третью в точке В. Далее процесс повторяется. В результате получается ломаная. Верно ли, что она замкнется?
20. Биссектрисы противоположных углов некоторого четырехугольника попарно параллельны. Докажите, что данный четырехугольник — параллелограмм.
21. Вершины одного параллелограмма по одной лежат на сторонах другого. Докажите, что их центры совпадают. Центр параллелограмма—это точка пересечения его диагоналей.
22. Все углы шестиугольника равны. Докажите, что модули разностей длин его противоположных сторон равны.
1
В переводе с древнего греческого языка слово параллелограмм означает «вычерченный параллельными». Поэтому для его обозначения уместен знак #.