Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016

Медиана прямоугольного треугольника

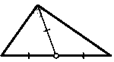
Свойство ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.

Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине его гипотенузы.

Признак прямоугольного треугольника. Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.

1. Докажите свойство прямоугольного треугольника.

2. Докажите признак прямоугольного треугольника.

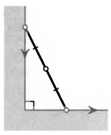
3. Прислоненная к вертикальной стене лестница начала падать, скользя по полу. Какую траекторию описывает ее середина?

4. В четырехугольнике два противоположных угла прямые, а диагонали перпендикулярны друг другу. Докажите, что одна из них делит другую пополам.

5. В четырехугольнике два противоположных угла прямые, а соединяющая их диагональ делится пополам другой диагональю. Докажите, что эти диагонали либо равны, либо перпендикулярны.

6. Диагонали четырехугольника перпендикулярны, а отрезок, соединяющий середины его противоположных сторон, равен среднему арифметическому этих сторон. Докажите, что данный четырехугольник-трапеция или ромб.

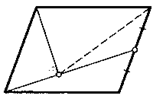
7. Вершину параллелограмма соединили с серединой его стороны. На полученный отрезок из другой вершины опустили перпендикуляр. Докажите, что пунктирный отрезок на рисунке равен стороне параллелограмма.

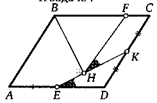
8. Точки Е и К — середины сторон AD и DC параллелограмма ABCD. Из его вершины В на прямую ЕК опустили перпендикуляр ВН. На стороне ВС выбрали точку F так, что углы FHK и KED равны. Найдите BF :FC.

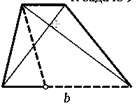
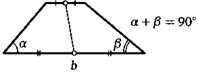
9. Найдите отрезок, соединяющий середины оснований трапеции, если сумма углов при одном из них равна 90°, а длины оснований равны а и Ъ.

10. Основания трапеции равны а и Ъ. Найдите отрезок, соединяющий середины оснований, если диагонали трапеции перпендикулярны.

11. Точка на одном основании трапеции находится на одинаковом расстоянии от концов ее диагонали. Найдите это расстояние, если диагонали трапеции перпендикулярны, а ее основания равны а и Ь.