Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016

Средняя линия треугольника

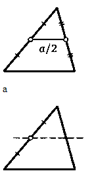
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Всего у треугольника три средние линии.

Теорема о средней линиии. Средняя линия треугольника параллельна его основанию и равна половине этого основания.

Признак средней линии. Если прямая параллельна стороне треугольника и делит одну его сторону пополам, то на этой прямой лежит средняя линия треугольника.

1. Где может находиться прямая, равноудаленная от всех вершин треугольника? Сколько всего таких прямых?

2. Прямая проходит через середину стороны треугольника и параллельна другой его стороне. Докажите, что она пересекает третью сторону треугольника в середине.

3. Вершину треугольника соединяют с произвольной точкой на противоположной его стороне. Докажите, что середины всех полученных отрезков лежат на одной прямой.

4. Отрезок с концами на двух сторонах треугольника параллелен третьей стороне и равен ее половине. Докажите, что этот отрезок — средняя линия треугольника.

5. (Теорема Вариньона.) В произвольном четырехугольнике отметили середины всех сторон. Докажите, что полученные точки образуют параллелограмм.

6. Диагонали четырехугольника равны. Докажите, что его средние линии⁴ перпендикулярны.

7. Известно, что средние линии четырехугольника равны. Докажите, что его диагонали перпендикулярны.

8. Докажите, что середины противоположных сторон четырехугольника и середины двух его диагоналей образуют параллелограмм (либо лежат на одной прямой).

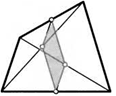
9. Докажите, что средние линии четырехугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке.

10. Противоположные стороны четырехугольника равны. Докажите, что прямая, проходящая через середины его диагоналей, образует с этими сторонами равные углы.

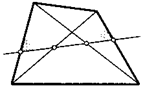
11. Средняя линия четырехугольника⁴ образует с его диагоналями равные углы. Докажите, что диагонали этого четырехугольника равны.

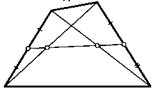
12. Диагонали четырехугольника равны, а одна из его средних линий в два раза их меньше. Найдите угол между диагоналями.

13. Две противоположные стороны четырехугольника равны 1. Найдите отрезок, соединяющий середины двух других его сторон, если сумма углов при одной из них равна 60°.

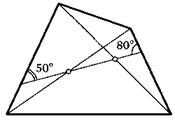
14. Прямая, проходящая через середины диагоналей четырехугольника, образует с его сторонами углы 50° и 80°. Докажите, что расстояние между серединами диагоналей равно половине одной из сторон четырехугольника.

15. Две противоположные стороны шестиугольника параллельны и равны. Докажите, что середины четырех остальных его сторон образуют параллелограмм.

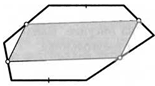
К задаче 16

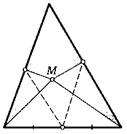
18. Внутри треугольника АВС взяли произвольную точку М. Середины отрезков AM, ВЫ и СМ соединили с серединами сторон ВС, АС и АВ треугольника соответственно. Докажите, что три полученных отрезка пересекаются в одной точке.

В

19. Докажите, что середины всех сторон треугольника и основание любой его высоты образуют равнобокую трапецию.

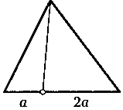
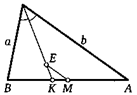
20. Сторона ВС треугольника равна а. Середину стороны АС соединили с точкой на стороне АВ так, что отмеченные на рисунке углы равны. Найдите МК.

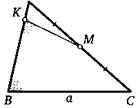
21. Гипотенуза прямоугольного треугольника равна с. Через середину его катета провели прямую, которая делит гипотенузу в отношении 1:3 так, как показано на рисунке. Найдите отрезок данной прямой, заключенный внутри треугольника.

22. Дан треугольник АВС, ВС = а, АС = Ь, а< Ъ. Через середину стороны АВ проводят прямую, параллельную АС, которая пересекая биссектрису СК в точке Е. Найдите ME.

С

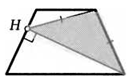
23. В трапеции ABCD основание AD в два раза больше основания ВС. Из вершины D на сторону АВ опустили перпендикуляр DH. Докажите, что треугольник СНВ равнобедренный.

ВаС

24. Разрежьте произвольный треугольник на три части, из которых можно сложить прямоугольник.

25. Разрежьте квадрат на три части так, чтобы из них можно было сложить треугольник без равных сторон и прямых углов.

26. Вершину треугольника соединили отрезком с серединой его медианы. Второй отрезок проходит через основание медианы и параллелен первому. Найдите отношение этих параллельных отрезков.

А 2а D

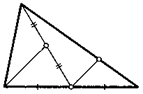
27. На двух сторонах треугольника вне его построили квадраты. Докажите, что их центры равноудалены от середины третьей его стороны

28. Два отрезка, соединяющие вершину параллелограмма с серединами не содержащих ее сторон, перпендикулярны. Найдите отношение диагоналей параллелограмма.

29. Постройте: а) треугольник; б) параллелограмм, если заданы середины всех его сторон.

30. Середины всех четырех звеньев ломаной являются вершинами параллелограмма. Докажите, что данная ломаная замкнута.

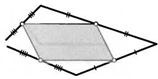
31. Постройте параллелограмм по одной вершине и серединам двух не содержащих ее сторон.

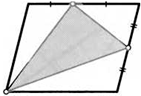
32. На доске нарисовали пятиугольник. Потом его стерли, но оставили середины всех сторон. Как по этим пяти точкам восстановить пятиугольник?

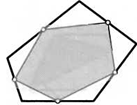
33. Тот же вопрос, что и в предыдущей задаче, но для семиугольника.

34. Середины четырех сторон пятиугольника соединили так, как показано на рисунке. Докажите, что расстояние между серединами двух полученных отрезков равно четверти одной из сторон пятиугольника.

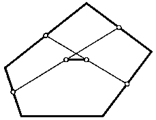
35. Восстановите пятиугольник по серединам всех его диагоналей.

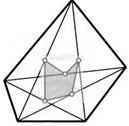
36. На всех сторонах треугольника взяли по точке (отличной от вершин). Каждую из них соединили с противоположной вершиной. Могут ли середины трех получившихся отрезков лежать на одной прямой?

37. Середины двух противоположных сторон четырехугольника соединили с его вершинами так, как показано на рисунке. Докажите, что середины полученных отрезков образуют параллелограмм.

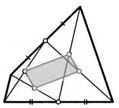
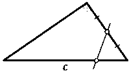
38. На биссектрисы двух углов треугольника из третьей его вершины опустили перпендикуляры. Найдите отрезок между основаниями этих перпендикуляров, если стороны треугольника равны а, b и с.

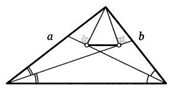
*39. В треугольнике взяли точку М так, что отмеченные на рисунке углы равны. Докажите, что основания перпендикуляров, опущенных из этой точки на боковые стороны треугольника, равноудалены от середины основания треугольника.