Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Теорема о средней линиии трапеции. Средняя линия трапеции параллельна ее основаниям и равна их среднему арифметическому.
Признак средней линии трапеции. Если прямая, параллельная основаниям трапеции, проходит через середину одной ее боковой стороны, то средняя линия трапеции лежит на этой прямой.
Е
а + Ь
Е
1. Возьмите середину диагонали трапеции. Докажите, что она лежит на ее средней линии.
2. Докажите теорему о средней линии трапеции.
3. Докажите признак средней линии трапеции.
4ч Отрезок с концами на боковых сторонах трапеции параллелен ее основаниям и равен их среднему арифметическому. Верно ли, что данный отрезок — средняя линия трапеции?
5. Найдите отрезок, соединяющий середины диагоналей трапеции, если ее основания равны а и Ь.
а

6. Средняя линия трапеции делится ее диагоналями на три равные части. Найдите отношение оснований трапеции.
7. Основание треугольника равно 1. Найдите отрезок, соединяющий середины его медиан, проведенных к боковым сторонам.
8. Концы произвольных отрезков лежат на двух параллельных прямых. Где могут находиться их середины?
9. Средняя линия четырехугольника равна полусумме двух его сторон, не имеющих с ней общих точек. Докажите, что данный четырехугольник — трапеция или параллелограмм.
10. Докажите, что биссектрисы углов при боковой стороне трапеции пересекаются на ее средней линии.
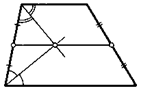
11. В трапеции провели биссектрисы всех углов. Найдите расстояние между отмеченными на рисунке точками их пересечения, если основания трапеции равны а и Ь, а боковые стороны —с и d.
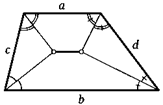
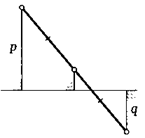
12. Расстояния от двух точек до некоторой прямой равны р и q. Найдите расстояние от середины соединяющего их отрезка до этой прямой, если точки находятся: а) по одну сторону от прямой; б) по разные стороны от прямой.
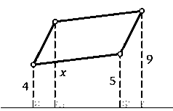
13. Прямая не пересекает сторон параллелограмма. Расстояния от трех его вершин до этой прямой равны последовательно 4, 5 и 9. Найдите расстояние до прямой от четвертой его вершины.
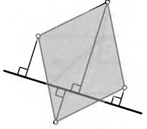
14. Прямая пересекает две соседние стороны параллелограмма. На нее из всех его вершин опущены перпендикуляры. Докажите, что один из них равен сумме трех других.
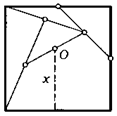
15. Сторона квадрата равна 1. Каждая из отмеченных на рисунке точек является серединой своего отрезка. Найдите отмеченное на рисунке пунктиром расстояние от точки О до стороны квадрата.
16. Два параллелограмма имеют общую вершину, а также по одной вершине на двух параллельных прямых, как показано на рисунке. Докажите, что отрезок, соединяющий оставшиеся две вершины, параллелен данным прямым.
