Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016

Окружность 2

Теорема. Геометрическим местом точек, из которых данный отрезок виден под прямым углом, является окружность, диаметр которой — данный отрезок⁶.

Теорема. Любой треугольник можно вписать в окружность. Серединные перпендикуляры ко всем его сторонам пересекаются в центре этой окружности.

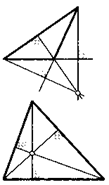
Теорема о высотах треугольника. Высоты любого треугольника (или их продолжения) пересекаются в одной точке.

Окружность Эйлера. Основания высот и середины сторон неравнобедренного треугольника лежат на одной окружности.

1. Дана окружность радиуса 2. Нарисуйте на плоскости все точки, расстояние от которых до какой-либо точки окружности не превосходит 1.

2. Дан отрезок длины 1. Нарисуйте все точки плоскости, расстояние от которых до какой-либо точки данного отрезка не превосходит 1.

3. Постройте окружность, проходящую через две данные точки, центр которой лежит на данной прямой.

4. Через точку внутри окружности проведите хорду так, чтобы она делилась данной точкой пополам.

5. Серединные перпендикуляры к трем сторонам четырехугольника пересекаются в одной точке. Докажите, что этот четырехугольник можно вписать в окружность.

6. В окружности провели две перпендикулярные хорды. Докажите, что расстояние между серединами этих хорд равно расстоянию от центра окружности до точки их пересечения.

7. Две хорды окружности равны. Докажите, что прямая, проходящая через их середины, образует с этими хордами равные углы.

8. Сторона клетки на рисунке равна 1. На каком расстоянии от прямой ВС находится центр окружности, проходящей через точки Л, В и С?

9. На двух сторонах треугольника как на диаметрах построили окружности. Докажите, что они пересекаются на его третьей стороне (или ее продолжении).

10. Два прямоугольника имеют общую вершину. Вокруг каждого из них описали окружность. Докажите, что вторая точка пересечения этих окружностей лежит на одной прямой с двумя вершинами прямоугольников.

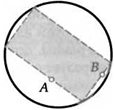
11. Внутри окружности даны точки А и В. Впишите циркулем и линейкой прямоугольник в эту окружность так, чтобы указанные точки лежали на двух его соседних сторонах.

12. Через точку внутри окружности проводятся произвольные хорды. Найдите геометрическое место их середин.

13. В окружность вписан параллелограмм. Докажите, что он является прямоугольником.

14. Центр описанной окружности треугольника лежит на его средней линии. Найдите больший из углов треугольника.

15. Сторона равностороннего треугольника равна 1. Найдите радиус окружности, проходящей через его вершину, середину противоположной стороны и середину еще одной стороны.

16. Точка Е — середина стороны ВС квадрата ABCD. Серединные перпендикуляры к отрезкам АЕ и ЕС пересекаются в точке О. Докажите, что она лежит на диагонали квадрата. Найдите ВО: OD.

ВЕС

A D

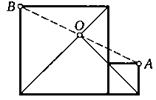
17. Два угла у квадратов на рисунке смежные. Продолжение диагонали одного квадрата пересекает диагональ другого в точке О. Докажите, что О — середина отрезка А£.

18. В окружность вписана трапеция. Докажите, что она равнобокая.

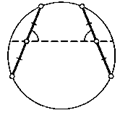
19. Докажите, что равнобокую трапецию всегда можно вписать в окружность.

20. (Окружность Эйлера.) Через середины сторон неравнобедренного треугольника проходит окружность. Докажите, что она вторично пересекает его стороны в основаниях высот.

21. Окружность проходит через середину гипотенузы и середину катета прямоугольного треугольника и пересекает другой его катет в двух точках. Первая из этих точек, расположенная ближе к вершине прямого угла, делит катет в отношении 1:4. В каком отношении делит этот катет вторая точка?

22. Точка А движется по окружности, точка В неподвижна. По какой траектории движется точка М — середина отрезка АВ?

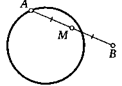
23. Две окружности пересекаются в точке М. Как циркулем и линейкой провести через точку М прямую так, чтобы она вторично пересекла эти

24. На основании АС треугольника АВС взяли точку М так, что угол СМВ равен 30°. Пусть О_г и 0₂ — центры описанных окружностей треугольников АВМ и СВМ. Докажите, что 0_г0₂ = АС.

В

AM С

25. Любые четыре вершины пятиугольника лежат на некоторой окружности. Докажите, что все пять его вершин лежат на одной окружности.

26. У пятиугольника есть три равных угла и две пары равных сторон, расположенных так, как показано на рисунке. Докажите, что этот пятиугольник можно вписать в окружность.

27. Пользуясь приведенным чертежом, докажите теорему о высотах треугольника.

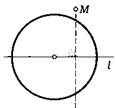
28. Даны окружность и прямая, проходящая через ее центр. С помощью только одной линейки опустите из данной точки М перпендикуляр на данную прямую.

I

29. В треугольнике АВС провели высоты AM и СК, которые пересеклись в точке Я. Точки О и Е — середины отрезков АС и ВН. Докажите, что прямые ОЕ и МК перпендикулярны.

30. В треугольнике АВС взяли такую точку М, что у треугольников ABM, СВМ и АСЫ равны радиусы описанных окружностей. Докажите, что М — точка пересечения высот треугольника.

31. К двум сторонам треугольника провели высоты. Через их основания провели прямую. На эту прямую из вершин третьей стороны опустили перпендикуляры. Докажите, что отмеченные на рисунке отрезки равны.

32. Два противоположных угла четырехугольника прямые. На соединяющую эти углы диагональ из двух других его вершин опустили перпендикуляры. Основания этих перпендикуляров делят данную диагональ на три отрезка. Докажите, что два из этих отрезков равны.

33. В окружность вписан квадрат ABCD. Через середины его сторон ВС и CD провели хорду КЕ. Докажите, что треугольник АКЕ равносторонний.

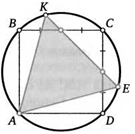
34. В окружности провели две перпендикулярные хорды АВ и CD. Докажите, что расстояние от центра окружности до хорды AD в два раза меньше хорды СВ.

В

*35. Через точку пересечения двух окружностей проводят произвольную прямую, которая вторично пересекает эти окружности в точках Л и Б. Найдите геометрическое место середин отрезков АВ.

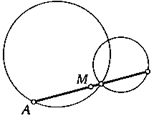
*36. Из середины каждой стороны вписанного четырехугольника на его противоположную сторону опущен перпендикуляр. Докажите, что четыре таких перпендикуляра пересекаются в одной точке.

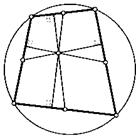
*37. На стороны АС и ВС треугольника АВС из середины его третьей стороны АВ опустили перпендикуляры. Основаниями этих перпендикуляров являются точки М и К соответственно. Вокруг треугольников АСК и ВСМ описали окружности. Найдите расстояние между центрами этих окружностей, если АВ = 1.

1

Поскольку трапеция в технике перспективы служила изображением стола, продолжения ее боковых сторон должны были пересекаться на «линии горизонта», то есть не могли быть параллельны.

2

Это свойство и аналогичный признак будут доказаны позже в теме «Касательные».

3

Многоугольник называют правильным, если у него равны все стороны и все углы.

4

Средней линией четырехугольника называют отрезок, соединяющий середины его противоположных сторон.

5

Обратная теорема в общем виде неверна.

6

Концы самого отрезка не входят в указанное множество, поскольку для них не определен указанный угол.