Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Касательные к окружности
Касательной к окружности называется прямая, имеющая с ней единственную общую точку. Если прямая касается сразу двух окружностей, то она называется их общей касательной. Различают внешнюю и внутреннюю касательные к двум окружностям. Если окружности лежат в одной полуплоскости от их общей касательной, то она называется внешней, если в разных полуплоскостях, то внутренней.

общая внешняя касательная
общая внутренняя касательная
Теорема о касательной. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

Ъ
а
d
<2 4- с = b + d
Обратная теорема о касательной. Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведенному в эту точку, то она является касательной.
Свойство отрезков касательных. Отрезки касательных, проведенных к окружности из одной точки, равны.
Свойство ОКРУЖНОСТИ, ВПИСАННОЙ В УГОЛ. Центр окружности, вписанной в угол, находится на биссектрисе угла.
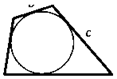
Свойство ОПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА. В четырехугольнике, описанном вокруг окружности, суммы длин противоположных сторон равны.
1. Докажите теорему о касательной.
2. Докажите обратную теорему о касательной.
3. Кресло-качалка, основание которого имеет форму дуги окружности, качается на горизонтальном полу. По какой траектории движется центр окружности?
4. Касательная параллельна хорде окружности. Докажите, что точка касания равноудалена от концов данной хорды.

5. а) Докажите свойство отрезков, касательных к окружности; б) Докажите свойство окружности, вписанной в угол.
6. Докажите свойство описанного четырехугольника. Что можно сказать о биссектрисах всех его углов?
7. Постройте окружность данного радиуса, вписанную в данный угол.
8. Постройте окружность, вписанную в данный угол и касающуюся одной его стороны в данной точке.
9. Даны две параллельные прямые и точка между ними. Постройте окружность, которая проходила бы через данную точку и касалась данных прямых. Сколько таких окружностей можно провести?
![]()
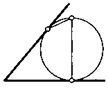
10. В угол вписана окружность. Через точку ее касания с одной из сторон угла провели диаметр. Другой конец диаметра соединили со второй точкой касания окружности. Докажите, что полученный отрезок параллелен биссектрисе угла.
11. Окружность касается всех сторон трапеции. Под каким углом из ее центра видны ее боковые стороны?
12. Окружность вписана в угол, причем расстояние между точками ее касания со сторонами угла равно радиусу. Найдите величину угла.
13. Две окружности вписаны в угол 60°, причем одна проходит через центр другой. Найдите отношение их радиусов.

14. На большем основании трапеции как на диаметре построили окружность. Оказалось, что она проходит через середины ее боковых сторон и касается другого основания. Найдите углы трапеции.

15. Прямая касается окружности радиуса 1 в точке А. Хорда АВ образует с касательной угол 60°. Найдите длину перпендикуляра, опущенного из точки В на касательную.
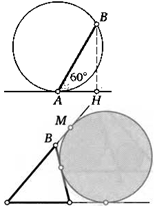
Л С К
АК=АМ=р/2
К задаче 15 К задаче 16
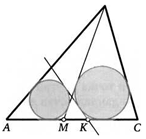
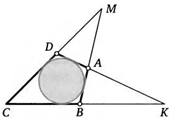
16. Окружность касается стороны ВС треугольника АВС и продолжений двух других его сторон в точках М и К. Докажите, что отрезки AM и АК равны половине периметра треугольника.
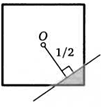
17. Сторона квадрата равна 1. Прямая проходит на расстоянии 1/2 от его центра и отсекает от квадрата треугольник. Найдите периметр этого треугольника.
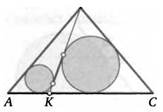
18. (Формула для отрезка касательной окружности, вписанной в треугольник.) В треугольник вписана окружность. Докажите, что расстояние х от его вершины до ближайшей к ней точк а+Ь—с, касания, указанное на рисунке, равно —^— =Р~С> гДе я, Ь, с — стороны треугольника, ар — половина периметра треугольника.

19. На основании АС равнобедренного треугольника АВС взяли точку К. В треугольники АВК и СВК вписали окружности. Найдите расстояние между точками касания этих окружностей с отрезком ВК, если АК — 2,СК = 5.
В
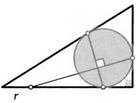
20. Окружность касается одной стороны треугольника и продолжений двух других. Найдите указанное на рисунке расстояние х от его вершины до одной из точек касания, если стороны треугольника равны а, Ъ, с.

21. Найдите радиус окружности, вписанной в прямоугольный треугольник со сторонами 3, 4, 5.
18
22. Стороны прямоугольного треугольника равны 3, 4, 5. Найдите радиус окружности, касающейся его гипотенузы и продолжений двух катетов.
23. В прямоугольный треугольник вписана окружность. Через точку ее касания с катетом проведена прямая, перпендикулярная хорде, соединяющей две другие точки касания. Эта прямая разбивает второй катет на два отрезка. Докажите, что меньший из них равен радиусу данной окружности.
24. Каждая из двух окружностей касается боковой стороны треугольника и продолжений двух других. Докажите, что отмеченные на рисунке отрезки равны.
25. Пятиугольник описан вокруг окружности, причем все его стороны равны. Докажите, что все углы пятиугольника тоже равны.
26. Одна из сторон треугольника равна с. В противоположный от нее угол вписаны две окружности, которые касаются данной стороны в двух точках. Найдите расстояние между этими точками, если две другие стороны треугольника равны а и Ъ.

а
27. В обозначениях предыдущей задачи найдите расстояние между точками касания двух данных окружностей с одной из сторон угла.
28. Две стороны треугольника равны 5 и 7. В угол, образованный этими сторонами, вписаны две окружности, которые касаются третьей стороны треугольника в двух точках. Найдите его третью сторону, если указанные точки делят ее на три равные части.
29. Окружность касается всех сторон четырехугольника ABCD. Продолжения его противоположных сторон АВ и CD пересекаются в точке М, а продолжения сторон ВС и AD — в точке К. Докажите, что BK + BM = DK + DM.
30. Окружность касается двух сторон треугольника и двух медиан, проведенным к этим сторонам. Докажите, что данный треугольник равнобедренный.
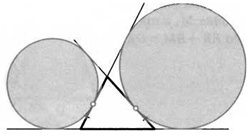
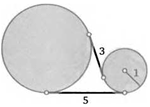
31. Радиус одной из окружностей равен 1. Найдите радиус другой окружности, если длины отрезков их общих внутренней и внешней касательных равны 3 и 5.
*32. На стороне АС треугольника АВС взяли произвольную точку М. В треугольники АВМ и СВМ вписали окружности. Общая внутренняя касательная к этим окружностям, отличная от прямой ВМ, пересекает АС в точке К. Докажите, что точка К не зависит от выбора точки М.
В