Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Первый признак равенства треугольников
Многоугольники называются равными, если можно совместить все их соответствующие стороны и углы4. Из определения очевидно следует, что у двух равных многоугольников соответственно равны все стороны и все углы.

Аксиома «прикладывания треугольника к лучу». К любому лучу можно приложить треугольник, равный данному, так, чтобы первая его вершина совпала с началом луча, вторая лежала на луче, а третья оказалась в нужной полуплоскости относительно прямой, на которой лежит луч. А В
Данная аксиома нужна для того, чтобы при доказательствах признаков равенства треугольников была возможность прикладывать один треугольник к другому нужным нам образом — так, как если бы они были вырезаны из бумаги.
А\
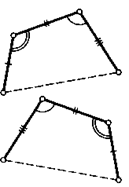
Первый признак равенства треугольников.
Если две стороны и угол между ними в одном треугольнике соответственно равны двум сторонам и углу между ними в другом треугольнике, то такие треугольники равны.
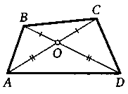
1. Диагонали четырехугольника ABCD пересекаются в точке О. Известно, что АО = OD, ВО = ОС, Докажите, что АВ = CD.
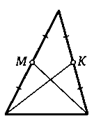
2. Точки МиК — середины равных сторон АВ и ВС треугольника АВС. Докажите, что АК = СМ.
В
А С
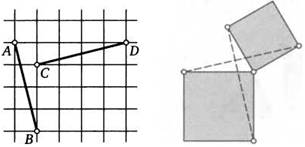
К задаче 2 К задаче 4 К задаче 6
3. Все стороны и все углы пятиугольника равны. Докажите, что равны все его диагонали.
4. На клетчатой бумаге нарисовали отрезки АВ и CD так, как показано на рисунке. Докажите, что они равны.
5. Отрезки АВ и CD пересекаются в точке О, которая является серединой каждого из них. Докажите, что ZCAD = ZCBD.
6. Два квадрата имеют общую вершину. Докажите, что отмеченные пунктиром на рисунке отрезки равны (по определению у квадрата все стороны равны, а углы прямые).
7. Три квадрата расположены так, как показано на рисунке. Докажите, что отрезки АВ и CD равны.

К задаче 7 К задаче 8 К задаче 9
8. В пятиугольнике ABCDE углы АВС и CDE равны, АВ = ED, BC = CD. Докажите, что равны отрезки AD и BE.
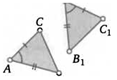
9. Точки Л и В отразили относительно прямой. Получились точки А1 и Вг. Докажите, что АВ = А1В1.
10. У двух четырехугольников соответственно равны три стороны и два угла между этими сторонами. Докажите, что у них равны и четвертые стороны.