Геометрия 7 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015 год
ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ - Урок 2 - ТРЕУГОЛЬНИКИ
|
Цель деятельности учителя |
Совершенствовать навыки решения задач на применение второго признака равенства треугольников |
||
|
Термины и понятия |
Треугольник, прилежащие углы |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют работать с геометрическим текстом (анализировать его, извлекать необходимую информацию) |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: осознают важность и необходимость изучения предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные ресурсы |
• Тестовые задания |
||
|
I этап. Актуализация опорных заданий учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить теоретический уровень усвоения материала |
(И) 1. Доказательство второго признака равенства треугольников. (К доске вызывается один из учащихся, ответ его заслушивается всем классом.) (Ф) 2. Фронтальная работа с классом - тестовые задания обучающего характера с последующей самопроверкой.
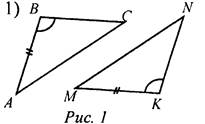
Для доказательства равенства треугольников АВС и MNK достаточно доказать, что: a) AC = MN; б) ∠C = ∠N; в) ВС = NK.
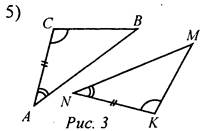
Для доказательства равенства треугольников АВС и EDF достаточно доказать, что: a) АС = FE; б) ∠C = ∠E; b) ∠A = ∠F. 3) Чтобы доказать равенство равносторонних треугольников АВС и MNK, достаточно доказать, что: a) ∠A = ∠M; б) АВ = MN; в) РABC = РMNK. 4) Чтобы доказать равенство двух равнобедренных треугольников TOS и DEF с основаниями TS и DF соответственно, достаточно доказать, что: а) ∠O = ∠E; б) TS = DF и ∠T = ∠D; в) TS = DF.
Выберите верное утверждение: а) ВС = КМ; б) AB = KN; в) ВС = NM. Ответы: 1 - в; 2 - б; 3 - б; 4 - б; 5 - а |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения задач |
(Г) Организует деятельность учащихся. Учащиеся распределяются в группы по 3-4 человека и решают задачи № 130, 131, 133, выполняя рисунки и записывая краткие решения. Учитель контролирует правильность решения задач в группах, при необходимости консультирует как целые группы, так и отдельных учащихся. Группы презентуют свои решения |
№ 130.
Дано: ΔАВС и ΔА1В1С1, СО, С1О1 - медианы, BC = B1C1, ∠B = ∠B1, ∠C = ∠C1. Доказать: 1) ΔАСО = ΔA1C1О1; 2) ΔВСО = ΔВ1С101. Доказательство: 1) Рассмотрим ΔАВС и ΔА1В1С1. ВС = В1С1 (по усл.), ∠B = ∠B1 (по усл.), ∠C = ∠C1 (по усл.). ΔАВС = ΔА1В1С1 (по сторонам и двум углам). АВ = А1В1, ∠А = ∠А1, АС = А1С1 (по определению равных треугольников). 2) Рассмотрим ΔАОС = ΔА1О1С1. АС = А1С1 (из п. 1), ∠А = ∠А1 (из п. 1). АО = А1С1 (так как ΔАОС = ΔА1О1С1 (по двум сторонам и углу между ними). 3) Рассмотрим ΔВСО = ΔВ1С1О1. ВС = В1С1 (по усл.), АВ = АВ1 (по усл.), ОВ = О1В1 (так как ΔВСО = Δ В1С1О1 (по двум сторонам и углу между ними). № 131.
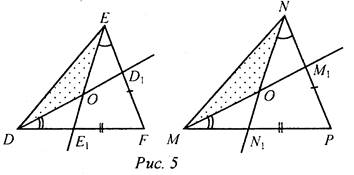
Дано: ΔDEF и ΔMNP, EF = NP, DF = МР, ∠F = ∠P, EE1, DD1 - биссектрисы, ЕЕ1 ∩ DD1 = O, MM1∩ NN1 = K. Доказать: ∠DOE = ∠MKN. Доказательство: 1) Рассмотрим ΔDEF и ΔMNP. EF = NP (по усл.), DF = МР (по усл.), AF = АР (по усл.). ΔDEF = ΔMNP (по двум сторонам и углу между ними), тогда ∠D = ∠M, ∠Е = ∠N, DE = MN (по определению равных треугольников). 2) Рассмотрим ΔDOE и ΔMNK. DE = MN (из п. 1), ΔEDO = ΔNMK (так как ∠DEO = ∠MNK (так как ΔDOE = ΔMKN (по стороне и двум прилежащим углам), тогда ∠DOE = ∠MKN (по определению равных треугольников). № 133.
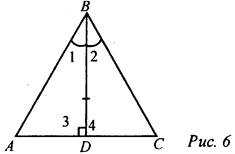
Дано: ΔАВС, BD - биссектриса. Доказать: ΔАВС - равнобедренный. Доказательство: Рассмотрим ΔABD и ΔCBD: BD - общая, ∠1 = ∠2 (так как BD — биссектриса), ∠3 = ∠4 (так как BD - высота). ΔABD = ΔCBD (по стороне и двум прилежащим углам). АВ = ВС (по определению равных треугольников), значит, ΔАВС - равнобедренный |
|
|
III этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Оцените свою работу. - Оцените работу в группе |
(И) Домашнее задание: решить 129, 132, 134 |
||