Алгебра 8 класс - Технологические карты уроков по учебнику А. Г. Мордковича - 2016
КОНТРОЛЬНАЯ РАБОТА № 6 - КВАДРАТНЫЕ УРАВНЕНИЯ
|
Цели деятельности учителя |
Проконтролировать умения решать квадратные, рациональные, биквадратные уравнения |
|
Тип урока |
Контроль знаний учащихся |
|
Планируемые образовательные результаты |
Предметные: знать понятия: “квадратное уравнение”, “алгоритм решения квадратного уравнения”, “рациональное уравнение”, “биквадратное уравнение”. Личностные: формирование ответственного отношения к успешной учебной деятельности. Метапредметные: регулятивные - уметь планировать свою деятельность, осуществлять самоконтроль и самооценку, оценивать результат; познавательные - уметь работать по правилу, алгоритму, аналогии, прогнозировать, анализировать, концентрировать внимание на главном |
|
Основные понятия |
Рациональные уравнения, квадратные уравнения, биквадратные уравнения, простейшие уравнения с параметрами |
|
Ресурсы |
Учебник |
|
Организация пространства |
Самостоятельная |
Урок 88. Контрольная работа № 6
|
Технология проведения |
Деятельность учителя |
Задания для учащихся, выполнение которых приведет к достижению запланированных результатов |
Деятельность учеников |
Планируемые результаты |
|
|
предметные |
универсальные учебные действия (УУД) |
||||
|
I. Организационный момент. Цели: создать деловой настрой для занятия; информировать о подготовке к уроку |
Приветствует учащихся, отмечает устно их готовность к проведению урока |
Концентрация внимания на необходимых действиях |
Слушают учителя, отвечают на вопросы |
Уметь сосредоточиться на определенном вопросе по математике |
Регулятивные: уметь ориентироваться в требованиях к уроку математики |
|
II. Проверка домашнего задания. Цели: актуализировать знания для устранения подобных ошибок; создать условия для повторения основных понятий |
Руководит проверкой домашней работы. Организует уточнение типа урока и называние шагов учебной деятельности |
Устная проверка домашней работы |
Отвечают на вопросы. Проговаривают правила при необходимости. Читают ответы устно |
Знать определение рационального уравнения, алгоритм решения такого уравнения |
Познавательные: уметь ориентироваться в своей системе знаний, структурировать знания; использовать знаково-символические средства. Коммуникативные: уметь формулировать известные правила в устной и письменной формах |
|
III. Решение контрольной работы. Цели: проконтролировать выполнение учащимися базовых учебных действий; выявить уровень усвоения темы |
Организует общую работу над решением заданий контрольной работы |
Контрольная работа (задания - см. Приложение к уроку 88) |
Решают задания в тетрадях |
Знать теоретически понятие о квадратных уравнениях. Уметь решать различные квадратные уравнения |
Познавательные: уметь ориентироваться в необходимых формулах, работать по алгоритму и аналогии. Регулятивные: уметь прогнозировать ситуацию, осуществлять самоконтроль и самооценку |
|
IV. Подведение итогов учебной деятельности, домашнее задание. Цель: нацелить на выполнение домашнего задания |
Выставляет оценки для учащихся, раньше времени выполнивших контрольную работу. Говорит о домашнем задании |
Домашнее задание: Работа с учебником: с. 158-164. Повторить алгоритмы решения квадратного уравнения, рационального уравнения и метод введения новой переменной |
Слушают учителя, записывают домашнее задание, задают вопросы по необходимости |
Уметь выявлять аналогию предметных действий |
Регулятивные: уметь прогнозировать ситуацию. Личностные: уметь выполнять оценку и самооценку деятельности |
Приложение к уроку 88
Контрольная работа № 6
Вариант 1
1. Определите число корней уравнения:
![]()
2. Решите уравнение:
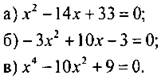
3. Одна сторона прямоугольника на 9 см больше другой. Найдите стороны прямоугольника, если его площадь равна 112 см2.
4. Решите уравнение: 
5. При каких значениях параметра р уравнение 4x2 + рх + 9 = 0 имеет один корень?
Вариант 2
1. Определите число корней уравнения:
![]()
2. Решите уравнение:
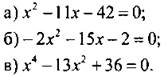
3. Один катет прямоугольного треугольника на 5 см меньше другого. Найдите длину каждого катета, если площадь этого треугольника равна 42 см2.
4. Решите уравнение: ![]()
5. При каких значениях параметра р уравнение х2 - рх + р = 0 имеет один корень?