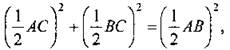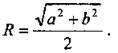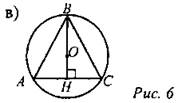Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПЛОЩАДЬ КРУГА - ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
|
Цель деятельности учителя |
Создать условия для выведения формулы для вычисления площади круга |
|||
|
Термины и понятия |
Круг, площадь круга |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют систематическими знаниями о плоских фигурах и их свойствах |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации. Регулятивные: проявляют учебную компетентность; умеют контролировать процесс и результат учебной математической деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: проявляют познавательный интерес к изучению предмета |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Исторические сведения о квадратуре круга; • задание для фронтальной работы |
|||
|
I этап. Актуализация опорных знаний учащихся |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Выявление трудностей, возникших при выполнении домашнего задания |
(Ф/И) 1. Ответить на вопросы учащихся. 2. Проверить на доске решение № 1107 и 1111. № 1107.
Ответ: 12 739 км. № 1111.
Дано: Окр (0; R), d = 58 см, ∠AOB = 117°. Найти: длину дуги. Решение:
Ответ: 59,2 см |
|||
|
II этап. Учебно-познавательная деятельность |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Ввести понятие круга, вывести формулу площади круга |
(Ф) 1. Ввести понятие круга. 2. Вывести формулу площади круга. 3. Записать в тетрадях: “Для вычисления площади S круга радиуса R применяется формула: S = πR2”. 4. Историческая справка. В течение веков усилия многих математиков были направлены на решение задачи, получившей название “Задача о квадратуре круга”: построить при помощи циркуля и линейки квадрат, площадь которого равна площади данного круга. Только в конце XIX века было доказано, что такое построение невозможно |
|||
|
III этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
На простейших примерах закрепить применение полученной формулы |
(Ф/И) Организует деятельность учащихся. 1. Решить задачу. На здании МГУ установлены часы с круговым циферблатом, имеющим диаметр примерно 8,8 м. Найдите площадь циферблата этих часов и сравните с площадью вашей классной комнаты. Ответ: 60,8 м2. 2. Решить задачу № 1118 (самостоятельно). 3. Решить задачу № 1119 на доске и в тетрадях. 4. Решить задачу № 1125 на доске и в тетрадях. 5. Решить задачу № 1116 на доске и в тетрадях |
№ 1119
Дано: круг (О; R), С = 41 м. Найти: d и S. Решение: 1) С = 2πR, так как 2r = d, то 41 = πd, d = 41 : 3,14 ≈ 13,02 м. 2) S = пr2 = 3,14 ∙ 6,52 = 133,84 м2. Ответ: 13,02 м, 133,84 м2. № 1125
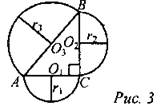
Дано: ∆АВС, ∠C = 90°, АС - диаметр Окр (O1; r1); ВС - диаметр Окр (O2; r2); AB - диаметр Окр (O3; r3). Доказать: S3 = S1 + S2. Доказательство:
№ 1116. a)
Дано: ABCD - прямоугольник вписан в круг (О; R), АВ = а, ВС = b. Найти: S круга. Решение:
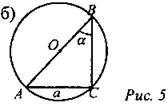
Дано: ∆АВС - вписан в круг (О; R), ∠C = 90°, АС = a, ∠B = α. Найти: S круга. Решение:
Дано: ∆АВС - вписан в круг, АВ = ВС, АС = а, ВН ⊥ АС, ВН = h. Найти: S круга. Решение: 1) если АО = R, то ОН = h - R, по теореме Пифагора: АО2 = ОН2 + АН2.
|
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Задайте три вопроса по теме урока. - Составьте синквейн к уроку |
(И) Домашнее задание: если в классе не успели доделать № 1116, то закончить дома; решить №1114, 1115 |
|||