Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
РЕШЕНИЕ ЗАДАЧ - Урок 4 - ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
|
Цель деятельности учителя |
Создать условия для закрепления знаний учащихся по изученной теме “Длина окружности и площадь круга”, для обучения применению изученных формул при решении задач; способствовать развитию логического мышления |
||
|
Термины и понятия |
Круг, площадь круга, круговой сектор, площадь кругового сектора, круговой сегмент, длина окружности, длина дуги окружности |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют систематическими знаниями о плоских фигурах и их свойствах |
Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем, контролировать процесс и результат учебной математической деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); парная (П); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Тест; • задания для парной и самостоятельной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Выявить уровень сформированности теоретических знаний |
(Ф/И) 1. Повторить определения окружности, круга, кругового сектора и кругового сегмента. 2. Записать на доске и в тетрадях формулы для вычисления длины окружности, длины дуги окружности, площади круга, площади кольца, площади кругового сектора. 3. Выполнить устный тест; 1) Установите, истинны или ложны данные высказывания: а) Длину окружности можно вычислить по формуле С = πD, где D - радиус окружности. б) Площадь круга равна произведению квадрата его радиуса на π. в) Длина полуокружности диаметра 10 равна 5π. г) Площадь круга можно вычислить по формуле д) Площадь круга радиуса 10 равна 10π. е) Длина дуги окружности с градусной мерой в 60° вычисляется по формуле ж) Площадь кругового сектора, ограниченного дугой в 90°, вычисляется по формуле з) Если длина дуги окружности радиуса R равна πR/4, то градусная мера этой дуги равна 90°. 2) Закончите предложение: а) Если диаметр окружности равен 6см, то ее длина... б) Если диаметр круга увеличить в 4 раза, то его площадь увеличиться в... в) Если радиус окружности уменьшить на 3, то ее длина уменьшится на... г) Если радиус круга равен 6 см, то площадь его кругового сектора вычисляется по формуле... д) Площадь вписанного в окружность квадрата со стороной 16 см, а площадь круга, ограниченного данной окружностью... е) Площадь описанного около окружности правильного четырехугольника равна 25. Длина этой окружности равна... ж) Диаметр окружности равен 8 см. Периметр правильного шестиугольника, вписанного в окружность равен... 3) Сторона правильного четырехугольника, вписанного в окружность, равна 10. Длина окружности равна... Ответы: 1) Истинные высказывания: б, в, ж. Ложные высказывания: а, г, д, е, з. 2) а) 6π; б) 16; в) 6π; г) πα/10; д) 8π; е) 5π; ж) 24; з) 10√2π. 4. Проверить домашнее задание: на доске решены № 1121 и 1124 с ошибками. Задание - найти ошибки, объяснить их и исправить |
||
|
II этап. Решение задач |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навыки решения задач |
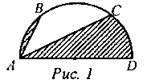
(П) Учащиеся работают в парах, затем представляют и обсуждают свои решения. 1. Решить задачи № 1116, 1123. 2. На рисунке изображен полукруг с диаметром AD. ∪АВ = ∪CD. ∪BC = 90°. Плошадь заштрихованной фигуры равна 16π. Найти длину дуги ВС
|
||
|
III этап. Самостоятельная работа |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Проверить умение применять изученные формулы при решении задач |
(И) Вариант I 1. Длина окружности равна 8л. Вычислите площадь круга, ограниченного данной окружностью. 2. Градусная мера дуги окружности с радиусом 6 см равна 30°. Вычислите площадь кругового сектора, соответствующего этой дуге. Вариант II 1. Длина окружности равна Юл. Вычислите площадь круга, ограниченного данной окружностью. 2. Градусная мера дуги окружности с радиусом 4 см равна 45°. Вычислите площадь кругового сектора, соответствующего этой дуге. Ответы: Вариант I: 1) 16π; 2) 3π см2. Вариант II: 1) 25π; 2) 2π см2 |
||
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Какие формулы повторили на уроке? - Оцените свою работу на каждом этапе урока |
(И) Домашнее задание: № 1132, 1137 |
||