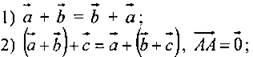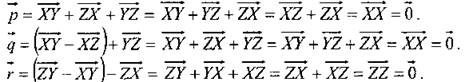Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
СУММА НЕСКОЛЬКИХ ВЕКТОРОВ. ВЫЧИТАНИЕ ВЕКТОРОВ - ВЕКТОРЫ
|
Цель деятельности учителя |
Создать условия для введения понятий суммы трех и более векторов, разности векторов, для обучения построению суммы двух и нескольких векторов с использованием правила многоугольника, разности векторов |
|||
|
Термины и понятия |
Вектор, сумма векторов, правило треугольника, правило параллелограмма, правило многоугольника, разность векторов |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Умеют применять векторы, находить сумму и разность векторов, строить сумму и разность векторов |
Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации. Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей. Коммуникативные: выстраивают аргументацию, участвуют в диалоге. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Задания для самостоятельной работы |
|||
|
I этап. Актуализация опорных знаний |
||||
|
Цель деятельности |
Задания для самостоятельной работы |
|||
|
Выявить уровень усвоения теоретического материала |
(Ф) 1. Решение задач (устно). 1) Найдите вектор х из условия:
2) Упростите выражение:
(И) 2. Самостоятельная работа (письменно). Работа выполняется на листках и сдается учителю на проверку. Вариант I 1. Начертите четыре попарно неколлинеарных вектора 2. Упростите выражение: Вариант II 1. Начертите пять попарно неколлинеарных векторов 2. Упростите выражение: |
|||
|
II этап. Работа по учебнику |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Развивать умения работать самостоятельно (используя текст учебника, разобрать новый материал) |
(И/Ф) 1. Используя рис. 253, разобрать сложение нескольких векторов. 2. Дать понятие о том, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. 3. По рис. 254 в учебнике рассмотреть построение суммы шести векторов. 4. Определить, в чем заключается правило многоугольника сложения нескольких векторов. 5. Записать в тетради правило многоугольника: если A1, А2, ..., Аn - произвольные точки плоскости, то 6. Рассмотреть рис. 255 (а, б). При сложении нескольких векторов сумма данных векторов может быть равна нулевому вектору, если начало первого вектора совпадает с концом последнего вектора |
|||
|
III этап. Мотивация к деятельности |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Дать задания, способствующие пониманию новой темы |
(Ф) - Что значит из числа а вычесть число b? - Найдите вектор - Сформулируйте правило вычитания двух отрицательных чисел. - Укажите вектор, противоположный вектору - Упростите выражение: |
|||
|
IV этап. Учебно-познавательная деятельность |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Ввести понятие разности векторов и научить строить разность векторов |
(Ф) 1. Предложить учащимся самим сформулировать определение разности двух векторов. 2. Дать определение разности двух векторов (формулирует учитель): 3. Рассмотреть задачу о построении разности двух векторов (рис. 256). 4. Ввести понятие вектора, противоположного данному (рис. 257). 5. Провести доказательство теоремы о разности векторов: для любых векторов |
|||
|
V этап. Решение задач |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Совершенствовать навыки решения задач |
(Ф/И) 1. Выполнить на доске и тетрадях практическое задание № 755, 756. 2. Решить задачу № 761 (без чертежа). 3. Решить № 762. 4. Решить задачу № 766 по рис. 259 (устно). 5. Решить задачу № 764 (а) на доске и в тетрадях. 6. Решить № 765 и 772 |
№762.
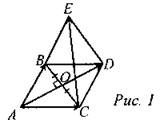
Дано: ∆АВC - равносторонний со стороной а. Найти:
Решение:
б) Проведем CD ll АВ и BD ll АС. ABCD - параллелограмм (по определению) и смежные стороны АВ = АС = а, значит, ABCD - ромб. По правилу параллелограмма Из прямоугольного ∆АОС (∠O = 90°) по теореме Пифагора:
в) Проведем DE ll BС и DE = ВС. Тогда г) По правилу треугольника: д) По правилу треугольника: Ответ: а; а√3; а√3; а; а. № 765. Воспользуемся правилами:
и тем, что
№ 772. Дано: ABCD - параллелограмм, X - любая точка плоскости. Доказать: Доказательство:
Получаем:
|
||
|
VI этап. Итоги урока Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(Ф/И) - Используя какие правила, можно найти сумму двух векторов, трех и более векторов? - Как найти разность векторов? - Составьте синквейн к уроку |
(И) Домашнее задание: № 760, 774, 757, 764(б), 767 |
|||
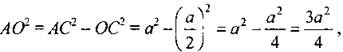 то есть
то есть