Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
|
Цель деятельности учителя |
Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала геометрии 7-9 классов |
|
|
Термины и понятия |
Основные понятия, свойства, признаки, теоремы, изученные в курсе геометрии 7-9 классов |
|
|
Планируемые результаты |
||
|
Предметные умения |
Универсальные учебные действия |
|
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость знаний в жизни человека |
|
|
Организация пространства |
||
|
Формы работы |
Индивидуальная (И) |
|
|
Образовательные ресурсы |
Задания для контрольной работы |
|
|
I этап. Выполнение контрольной работы |
||
|
Цель деятельности |
Задания для контрольной работы |
|
|
Проверить знания, умения, навыки по изученному материалу |
См. Ресурсный материал. Успешность выполнения теста можно оценить с помощью нижеперечисленных шкал: • удовлетворительно - 6-8 баллов; • хорошо - 9-11 баллов; • отлично - 12-14 баллов |
|
Ресурсный материал
Вариант I
Часть 1
1. В прямоугольнике диагонали пересекаются под углом 60°. Сумма диагонали меньшей стороны равна 24 см. Диагональ прямоугольника равна:
1) 12 см;
2) 16 см;
3) 12√3 см;
4) 16√3 см.
2. Вертикальный шест высотой 3 м дает тень длиной 1,5 м. Высота столба, тень от которого при таком же освещении составляет 6,5 м, равна:
1) 4,5 м;
2) 7,5 м;
3) 10м;
4) 13 м.
3. Стороны четырехугольника относятся как 2 : 4 : 3 : 6. Периметр подобного четырехугольника равен 120 см. Большая сторона второго четырехугольника равна:
1) 48 см;
2) 32 см;
3) 24 см;
4) 16 см.
4. В прямоугольной трапеции основания 4 см и 8 см, меньшая диагональ 2√13 см. Площадь трапеции равна:
1) 72 см2;
2) 36 см2;
3) 24 см2;
4) 12 см2.
5. Сторона треугольника, равная 4 см, лежит против угла, синус которого равен √3 - 1. Радиус описанной окружности равен:
1) √3 см;
2) √3 + 1 см;
3) √3 + 2 см;
4) 1 + 2√3 см.
6. В прямоугольном треугольнике катеты 5 см и 12 см. Длина окружности, вписанной в треугольник, равна:
1) 4π см;
2) 8π см;
3) 12π см;
4) 16π см.
7.
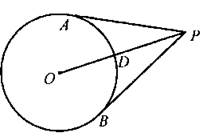
Из точки Р, отстоящей от окружности на 8 см, проведены касательные РА и РВ (см. рис.). Если РА + РВ = 24 см, то площадь круга равна _____ см2.
8. Площадь части круга радиусом R, расположенной вне вписанного в него квадрата, равна _______.
Часть 2
9. Стороны треугольника 3 см, 6 см и 7 см. Найдите длину биссектрисы большего угла треугольника.
Запишите ход решения и ответ на отдельном листе.
10. В круговой сектор с центральным углом 120° вписана окружность радиуса а. Найдите длину радиуса кругового сектора.
Запишите ход решения и ответ на отдельном листе.
Ответы:
Часть 1
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ответ: |
2 |
4 |
1 |
2 |
2 |
1 |
25π |
R2(π - 2) |
Часть 2
9.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Проведена биссектриса и дано правильное решение |
3 |
|
Ход решения верный, но допущены вычислительные ошибки |
2 |
|
Записано свойство биссектрисы и теорема косинусов |
1 |
|
Во всех остальных случаях |
0 |
Ответ: 8/3
10*.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Сделан чертеж и верные вычисления, могут отсутствовать объяснения |
3 |
|
Сделан чертеж, но в ходе решения допущены вычислительные ошибки и нет верного ответа |
2 |
|
Верный чертеж |
1 |
|
Во всех остальных случаях |
0 |
Ответ: 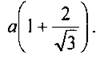
Вариант II
Часть 1
1. Хорда делит окружность в отношении 13:5. Больший из вписанных в окружность углов, опирающихся на эту хорду, равен:
1) 100°;
2) 130°;
3) 140°;
4) 150°.
2. В трапеции со средней линией 20 см через одну из ее вершин проведена прямая, параллельная боковой стороне и пересекающая среднюю линию в ее середине. Большее основание трапеции равно:
1) 10см;
2) 20 см;
3) 30 см;
4) 40 см.
3. Чтобы площадь круга увеличилась на 44 %, его радиус надо увеличить:
1) на 10 %;
2) 20%;
3) 30%;
4) 40%.
4. В прямоугольном треугольнике катеты 10 см и 24 см, Длина описанной окружности равна:
1) 13π см;
2) 14π см;
3) 20π см;
4) 26π см.
5. Диагонали ромба относятся как 2 : 3 и образуют с каждой стороной ромба треугольник, площадь которого равна 12 см2. Сторона ромба равна:
1) 10 см;
2) 16 см;
3) 2√13 см;
4) 2√14 см.
6. Если косинус угла, противолежащего стороне треугольника, равной 40 см, равен 0,6, то площадь описанного круга равна:
1) 25π см2;
2) 100π см2;
3) 125π см2;
4) 625π см2.
7. В прямоугольном треугольнике биссектриса острого угла делит катет на отрезки 4 см и 5 см. Площадь треугольника равна _____ см2.
8. В треугольнике со сторонами 3 см, 5 см и 6 см медиана, проведенная к большей стороне, равна ______.
Часть 2
9. В равнобедренной трапеции диагональ равна а и образует с основанием угол а. Найдите площадь трапеции.
Запишите ход решения и ответ на отдельном листе.
10. Высоты параллелограмма, проведенные из вершины тупого угла, равны 3 см и 5 см, а синус угла между ними равен 0,6. Найдите длину меньшей диагонали этого параллелограмма.
Запишите ход решения и ответ на отдельном листе.
Ответы
Часть 1
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ответ: |
2 |
3 |
2 |
4 |
3 |
3 |
54 |
2√2 |
Часть 2
9.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Сделан чертеж и дано верное решение, (могут отсутствовать подробные объяснения) |
3 |
|
Нет верного ответа, но сделан чертеж, выделен треугольник и найдены его катеты |
2 |
|
Сделан чертеж и записана формула для вычисления площади трапеции |
1 |
|
Во всех остальных случаях |
0 |
Ответ: a2 sin a cos а.
10*.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Сделан чертеж и дано верное решение |
3 |
|
Ход решений верный, но допущены вычислительные ошибки, могут отсутствовать объяснения |
2 |
|
Сделан чертеж и записана теорема косинусов для нахождения меньшей диагонали |
1 |
|
Во всех остальных случаях |
0 |
Ответ: 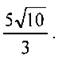
Вариант III
Часть 1
1. Если ![]() то длина вектора
то длина вектора ![]()
1) 3;
2) 4;
3) 5;
4) 6.
2. В квадрате ABCD сторона равна 2√2. Диагонали пересекаются в точке О. Скалярное произведение ![]() равно:
равно:
1) 8;
2) 4;
3) 2;
4) 1.
3. Средняя линия равнобедренного треугольника, параллельная боковой стороне, равна 13 см, а медиана, проведенная к основанию, — 24 см.
Длина средней линии, параллельной основанию треугольника, равна:
1) 2;
2) 10;
3) 50;
4) 100.
4. Вершины треугольника АВС делят описанную окружность в отношении 2:3:4. Меньший угол треугольника равен:
1) 20°;
2) 40°;
3) 60°;
4) 80°.
5. В треугольнике АВС стороны АВ, ВС и АС соответственно равны 3 см, 4 см и 6 см. Длина медианы ВМ равна:
1) 2√14;
2) √14;
3) 0,5√14;
4) 0,5√74.
6. Радиус вписанной в правильный треугольник окружности равен 3 см. Сторона треугольника равна:
1) 6;
2) 9;
3) 6√3;
4) 6√2.
7. В треугольнике АВС медиана AM перпендикулярна медиане BN. Найдите площадь треугольника АВС, если АМ = 2 см, BN = 3 см.
Ответ: ________________.
8. Площадь параллелограмма со сторонами 5 см и 8 см равна 32 см2. Найдите косинус большего угла параллелограмма.
Ответ: ________________.
Часть 2
9. ABCD - квадрат, длина его стороны равна 12 см. Точка К - середина стороны ВС, точка Р - точка пересечения прямых АК и BD. Найдите площадь треугольника ВКР.
Запишите ход решения и ответ на отдельном листе.
10. Диагональ равнобедренной трапеции делит тупой угол пополам. Меньшее основание трапеции равно 3 см, а ее периметр трапеции равен 42 см. Найдите площадь трапеции.
Запишите ход решения и ответ на отдельном листе.
Ответы:
Часть 1
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ответ: |
3 |
2 |
2 |
2 |
3 |
3 |
4 см2 |
-0,6 |
Часть 2
9.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Сделан чертеж и дано верное решение с объяснениями |
3 |
|
Сделан чертеж, ход решения верный, но допущены вычислительные ошибки |
2 |
|
Сделан чертеж, рассмотрены подобные треугольники, записано свойство площадей подобных треугольников |
1 |
|
Во всех остальных случаях |
0 |
Ответ: 12 см2.
10*.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Сделан чертеж и дано верное решение с объяснениями |
3 |
|
Сделан чертеж, ход решения верный, но допущены вычислительные ошибки |
2 |
|
Сделан чертеж, найдено второе основание, но не вычислена высота трапеции |
1 |
|
Во всех остальных случаях |
0 |
Ответ: 96 см2.
Вариант IV
Часть 1
1. Если ![]() то длина вектора
то длина вектора ![]() равна:
равна:
1) 6;
2) 8;
3) 10;
4) 100.
2. Сторона равностороннего треугольника АВС равна 4√3, М – середина AB, N – середина ВС. Скалярное произведение ![]() равно:
равно:
1) 6√3;
2) 8√3;
3) 12;
4) 24.
3. Средняя линия равнобедренного треугольника, параллельная основанию, равна 16 см, а биссектриса, проведенная к основанию, - 30 см.
Средняя линия треугольника, параллельная боковой стороне, равна:
1) 34;
2) 17;
3) 15;
4) 10.
4. Вершины треугольника АВС делят описанную окружность в отношении 1 : 3 : 5. Больший угол треугольника равен:
1) 40°;
2) 60°;
3) 80°;
4) 100°.
5. В треугольнике АВС стороны АВ, ВС и АС соответственно равны 2 см, 3 см и 4 см. Длина биссектрисы AD равна:
1) √5;
2) √6;
3) 5;
4) 6.
6. Радиус окружности, вписанной в правильный четырехугольник, равен 4 см. Сторона четырехугольника равна:
1) 6;
2) 8;
3) 4√2;
4) 8√2.
7. Найдите площадь треугольника АВС, если АВ = 27 см, ВС = 29 см и медиана ВМ = 26 см.
Ответ: _____________.
8. Длины сторон параллелограмма относятся 2 : 1, а синус его большего угла равен 0,32. Найдите площадь параллелограмма, если его периметр равен 75 см.
Ответ: _____________.
Часть 2
9. ABCD — квадрат со стороной 18 см. Точка Мделит сторону CD в отношении 2 : 1, считая от вершины С, точка Е - точка пересечения прямых AM и BD. Найдите площадь треугольника DEM.
Запишите ход решения и ответ на отдельном листе.
10. Диагональ равнобедренной трапеции равна 5 см, а ее средняя линия равна 4 см. Найдите площадь трапеции.
Запишите ход решения и ответ на отдельном листе.
Ответы:
Часть 1
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ответ: |
3 |
3 |
2 |
4 |
2 |
2 |
270 см2 |
100 см2 |
Часть 2
9.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Сделан чертеж и дано верное решение с объяснениями |
3 |
|
Сделан чертеж, ход решения верный, но допущены вычислительные ошибки |
2 |
|
Сделан чертеж, рассмотрены подобные треугольники, записано свойство площадей подобных треугольников |
1 |
|
Во всех остальных случаях |
0 |
Ответ: 13,5 см2.
10*.
|
Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) |
Баллы |
|
Сделан чертеж и дано верное решение с объяснениями |
3 |
|
Сделан чертеж, ход решения верный, но допущены вычислительные ошибки |
2 |
|
Сделан чертеж, найдено второе основание, но не вычислена высота трапеции |
1 |
|
Во всех остальных случаях |
0 |
Ответ: 12 см2.