Поурочные разработки по Алгебре 8 класс
Урок 1 - МОДУЛЬ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
Цели: ввести понятие модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля. Ввести функцию y = |x|; правила построения графиков, содержащих функцию y = |x|, правила решения и оформления уравнений, содержащих модуль; формировать умение работать с модулем.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Если самостоятельную работу в целом написали хорошо, то данные задания даются домой только тем учащимся, которые получили отрицательные оценки. Если же с работой не справились многие, то эти задания разбираются в классе.
1) Найти значение выражения: 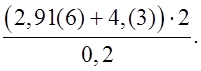
Р е ш е н и е:
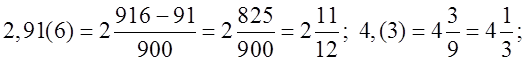
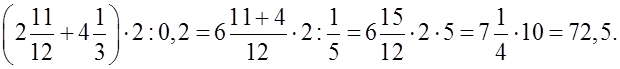
О т в е т: 72,5.
2) Сравнить числа: а) ![]() и 24; б)
и 24; б) 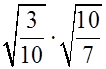 и
и 
3) Расставить числа в порядке убывания: ![]()
III. Объяснение нового материала.
1) Учитель предлагает вспомнить понятие модуля и найти значение выражения:
|34|, |–90|, 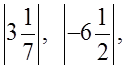 |–0,3|.
|–0,3|.
2) Далее вводится понятие модуля действительного числа, свойства модуля.
3) Разъясняется геометрический смысл модуля на геометрической модели – числовой прямой.
S(a, b) = |a – b|.
Модуль – это расстояние.
4) График функции y = |x| на доске строит один из учеников класса. Построение графика функции 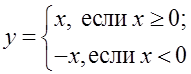 выполняется по точкам.
выполняется по точкам.
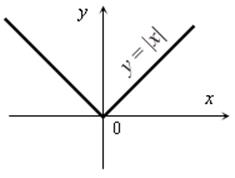
Выписать свойства данной функции:
1. Область определения (–; +).
2. y = 0 при x = 0, y > 0 при ![]()
3. Функция y = |x| является непрерывной.
4. Функция ограничена снизу, но не ограничена сверху.
5. ymin = 0 при x = 0; ymax не существует.
6. Данная функция убывает на интервале (–; 0] и возрастает на интервале [0; +).
7. Область значений данной функции луч [0; +).
5) Решение уравнения |x – 2| = 3 представить двумя способами:
а) Переведем аналитическую модель |x – 2| = 3 на геометрический язык:
на числовой прямой находим точки, которые удалены от точки 2 на расстояние, равное 3. Значит, уравнение имеет два корня: –1 и 5.
![]()
б) Построим на одной координатной плоскости два графика у = |x – 2| и у = 3.
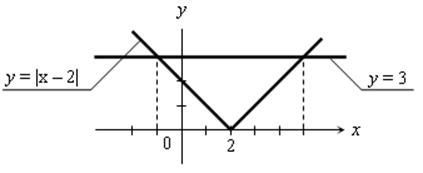
Абсциссы точек пересечения: –1 и 5.
IV. Закрепление нового материала.
1) Рассмотреть решение заданий № 16.2; 16.3; 16.4; 16.12; 16.16 (а, г); 16.19.
2) Повторить правила решения уравнений с модулями. Решить из учебника уравнения № 16.21; 16.23.
V. Подведение итогов.
Домашнее задание: прочитать материал параграфа 16, выучить правила данного параграфа. Решить задачи № 16.6; 16.11; 16.22.