Поурочные разработки по Алгебре 8 класс
Урок 2 - ФУНКЦИЯ y = ax2 + bx + c, ЕЁ СВОЙСТВА И ГРАФИК
Цели: повторить правила построения графика функции y = ax2 + bx + + c; рассмотреть свойства данной функции; развивать умение строить график квадратичной функции.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
К доске вызываются четыре учащихся для построения графиков данных функций:
Карточка 1 y = x2 – 4x |
Карточка 2 y = x2 – 6x + 3 |
Карточка 3 y = –3x2 + 12 |
Карточка 4 y = 2x2 + 8x – 5 |
III. Актуализация знаний.
Пока идет работа у доски, остальные учащиеся устно разбирают задания № 22.1; 22.2; 22.3; 22.4.
После проверки индивидуальных заданий, домашней работы, рассмотреть № 22.12, предварительно проведя фронтальный опрос:
1) Какая функция является квадратичной?
2) Приведите примеры квадратичных функций.
3) Параллельным переносом параболы можно получить график функции y = 2x2 – 3x, y = –x2 + 3x – 7, какой функцией задается эта парабола?
4) Куда направлены ветви данных парабол y = x2 – 4, y = 2x2 – 5x, y = –3x2 – 6x, y = 4x2 + 5x + 1?
5) Назовите числовые коэффициенты a, b, c следующих функций y = 2x2 – 6x + 1, y = x2 – 12x, y = 2x – x2 – 1?
IV. Решение задач.
1) Рассмотреть решения задач № 22.14; 22.16; 22.26 (а, г); 22.28 (б); 22.29 (б); 22.32; 22.41.
2) Найдите коэффициенты p и q у функции y = x2 + px + q, зная, что ее график проходит через точки A (2; –5) и B (–1; 16).
При наличии времени предложить задание: с помощью функций составить рисунок рожицы на координатной плоскости:
Голова:
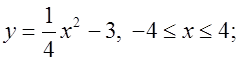

Рот:

Нос:
y = –x2 + 2, –1 ≤ x ≤ 1.
Глаза:
y = –x2 + 4x, 1 ≤ x ≤ 3; (–2; 3);
y = –x2 – 4x, –3 ≤ x ≤ –1; (2; 3);
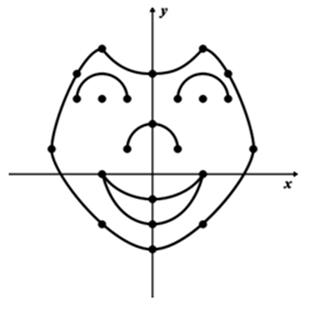
Для данной рожицы ученики сами могут попробовать дорисовать шапку и записать функцию, соответствующую графику.
V. Подведение итогов.
Домашнее задание: решить задачи № 22.15; 22.26 (б, в); 22.31; 22.44.