Урок 1 - ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ

Цели: закрепить умение строить графики различных функций; формировать умение решать квадратные уравнения графическим способом.

Ход урока

I. Организационный момент.

II. Обучающая самостоятельная работа.

Предлагаются следующие варианты:

Вариант 1	Вариант 2
№ 22.39 (а, г)	№ 22.39 (б, в)
№ 22.17 (а, г)	№ 22.17 (б, в)
№ 22.30 (а)	№ 22.30 (б)
№ 22.41	№ 22.44

Во время работы учитель помогает тем учащимся, которые не могут справиться с заданиями. Сложные для учеников задания рассматриваются на доске.

III. Объяснение нового материала.

Учитель показывает на доске решение квадратного уравнения x2 + 4x – 5 = 0 различными способами:

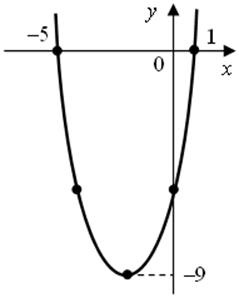
1) Для решения данного уравнения можно построить на координатной плоскости параболу функции y = x2 + 4x – 5 и найти точки пересечения данной параболы с осью Ox. Решением уравнения будут являться числа, соответствующие абсциссам точек пересечения. Решение показано на рисунке.

2) Можно часть выражения перенести на другую сторону таким образом, чтобы с одной стороны выражение составляло квадратичную функцию, а с другой стороны – линейную функцию.

Например x2 + 4x = 5, или x2 = 5 – 4x, или x2 – 5 = –4x. В этом случае нужно на одной координатной плоскости построить график квадратичной функции – параболу и график линейной функции – прямую. Значения абсцисс точек пересечения получившихся графиков и будут являться корнями данного уравнения.

3) Так же можно данное выражение разделить на переменную x, получив выражение 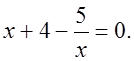В данном случае можно выражение разделить на две части, таким образом, чтобы с одной стороны осталось выражение, соответствующее линейной функции, тогда с другой стороны останется функция вида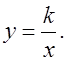

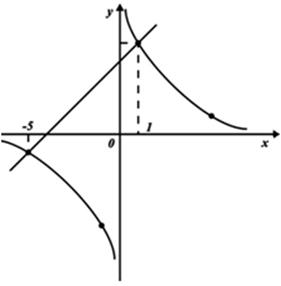
Например 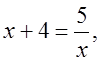или 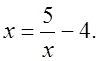На рисунке показано решение с помощью построения прямой y = x + 4 и гиперболы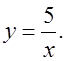

IV. Закрепление нового материала.

Рассмотреть решение уравнений № 23.1 (а, г); 29.2 (а, г); 23.5; 23.8 (а, г); 23.12 (а, г).

V. Подведение итогов.

Домашнее задание: решить задание № 23.4, пример (в) из заданий № 23.1; 23.2; 23.8; 23.12.