Поурочные разработки по Геометрии 11 класс
Объем шарового сегмента, шарового слоя, сектора - Объем шара и площадь сферы - ОБЪЕМЫ ТЕЛ
Цели урока:
- познакомить учащихся с формулами для вычисления объемов частей шара;
- научить учащихся решать задачи на применение формул объемов частей шара.
Ход урока
I. Организационный момент
II. Актуализация опорных знаний учащихся
- Площадь круга. Длина окружности. (S = πR2, С = 2πR = πD).
- Что называется сектором круга? Его площадью?
(Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. ![]() .)
.)
- Что называется сферой? Шаром? Центром, радиусом и диаметром шара? (Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.) (Шаром называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R, и не содержит других точек.)
- Что является сечением сферы? Шара? (Окружность, круг.)
- Что называется большим кругом шара?
- Объем шара.
III. Формирование новых знаний учащихся
1. Шаровым сегментом называется часть шара, отсеченная от него какой-нибудь плоскостью (рис. 1 а) и в)).
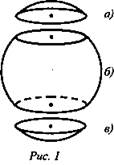
Круг, получившийся в сечении, называется основанием двух получившихся при этом сегментов.
Сегмент, в переводе с латинского (segmentum) отрезок (круга).
Длины отрезков АВ и ВС (рис. 2) диаметра АС, перпендикулярного секущей плоскости, называются высотами сегмента.
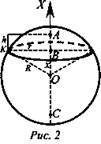
Если AB = h, a R- радиус шара, то ![]()
![]()
Докажем справедливость формулы (рис. 2). Проведем ось ОХ перпендикулярно плоскости α. Тогда площадь сечения S(x) = π(R2 - х2), при R - α ≤ х ≤ R.
Рассмотрим ΔКВО (∠β = 90°; ВО = х; КО = R). По основной формуле для вычисления объемов тел получим ![]()
![]()
2. Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.
Круги, получившиеся в сечении шара этими плоскостями, называются основаниями слоя, а расстояние между плоскостями - высотой шарового слоя.
![]()
3. Шаровым сектором называется тело, полученное вращением кругового сектора с углом меньшим 90°, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов (рис. 4).
![]()
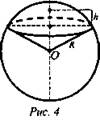
Сектор (от латинского sectio) - сечь, отделять, расчленять, делать отдельным.
IV. Формирование умений и знаний учащихся
Задача № 716. Работа в рабочих тетрадях. Один из учеников работает у доски, остальные в тетрадях (рис. 5).
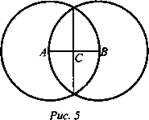
Решение:
1) Обозначим радиус шара через R, тогда АС = ВС = R/2. Общая часть шаров состоит из двух равных шаровых сегментов с высотой h = R/2.

(Ответ: 5/16.)
Задача № 718. Учащиеся работают самостоятельно, затем один из учащихся читает свое решение и записывает его на доске, остальные проверяют, исправляют ошибки (рис. 6).
Дано: шар, AD - диаметр, АВ = ВС = CD, R - радиус шара.
Найти: Vслоя.
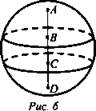
Решение: Vслоя = Vcerм.1 - Vcerм.2. Vcerм.1 = объем сегмента с высотой АC. AC = 4R/3. Vcerм.2 = объем сегмента с высотой АB. AB = 2R/3.
![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
Задача № 721.
Подробный разбор задачи и запись ее в тетради (рис. 7).
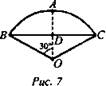
Решение: Пусть круговой сектор ОАВ вращается около радиуса ОА. В сечении получившегося шарового сектора плоскостью ОАВ получится еще один круговой сектор ОАС, симметричный исходному относительно прямой АО и имеющий тот же угол 30°. Угол БОС равен 60°, ОВ = OC = h, поэтому ΔBОС правильный, причем его сторона ВС отсекает от радиуса ОА отрезок AD, равный высоте Н соответствующего шаровому сектору сегмента. Найдем ее: ![]() Остается по формуле найти объем сектора:
Остается по формуле найти объем сектора: ![]() (Ответ:
(Ответ: ![]() )
)
V. Подведение итогов
- Какая часть шара называется шаровым сегментом, сектором?
Домашнее задание
П. 72, № 715, 717, 720.
Дополнительная задача
Диаметр шара, равный 30 см, служит осью цилиндра, у которого радиус основания равен 12 см. Найдите объем части шара, заключенный внутри цилиндра. (Ответ: 3528π см3.)