Повторение по теме: «Комбинации с описанными сферами» - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ

Цели урока:

- систематизировать теоретические знания о комбинациях тел;

- научить учащихся решать задачи на комбинации с описанными телами.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

Проверка домашнего задания. Провести взаимопроверку теста (ответы теста записать на доске).

№ варианта	1	2	3	4	5	6	7
1	г	б	а	г	а	в	а
2	в	б	в	в	б	в	б
3	в	а	в	а	а	б	в
4	а	б	в	б	б	а	а

III. Решение задач иа готовых чертежах

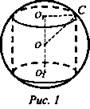
№ 1. Дано: ∠O1CO = 45°; O1С = 3√2 (рис. 1).

Найти: Vшар.

Ответ: 288π.

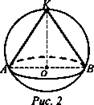
№ 2. Дано: КО = 6√3, ∠KBO = 60° (рис. 2).

Найти: Vшара

Ответ: 288π.

№ 3. Дано: KABCD – правильная пирамида, АС = АК = СК, ОС = 2√3.

Найти: Vпирамиды

Ответ: 6√3.

Пока учащиеся решают задачи на готовых чертежах, можно провести индивидуальную работу по карточкам (см. приложение).

Ответы:

I уровень:

II уровень:

III уровень:

Решения.

Карточка 1

Дано: В конус списана пирамида, АВ = ВС = АС, АО = R, ОК = Н (рис. 4).

Найти: Sбок. КАВС.

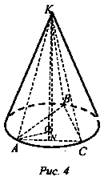
Решение: По теореме Пифагора Из ΔKON по теореме Пифагора

где а = R√3, тогда или (Ответ: )

Карточка 2

Дано: Около конуса описана пирамида АВ = ВС = AC, ОМ = R, КО = Н (рис. 5).

Найти: Sбок. КАВС.

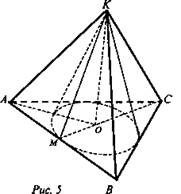
Решение: Из ΔКОМ по теореме Пифагора AO - биссектриса ∠CAB, тогда ∠OAB = 30°, АО = 2МО, АО = 2R (катет, лежащий напротив угла в 30° равен половине гипотенузы). Из ΔАОМ по теореме Пифагора тогда или (Ответ: )

Карточка 3

Дано: пирамида вписана в конус, ОК = Н, ∠AKC = α, АВ = ВС = CD = AD (рис. 6).

Найти: Sбок. КАВСD.

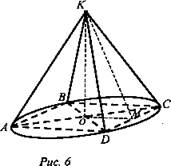
Решение: Так как ∠AKC = α, то ∠AKO = ∠CKO = α/2. По определению тангенса угла в ΔАОК: АО = ОС по свойству диагоналей квадрата, ΔACD равнобедренный, прямоугольный, по теореме Пифагора ОМ - средняя линия ΔADC, поэтому По теореме Пифагора из ΔОКМ

(Ответ: .

Карточка 4

Дано: конус вписан в пирамиду AB = BC = CD = AD, КМ = l, ∠KMO = α (рис. 7).

Найти: Sбок. КАВСD.

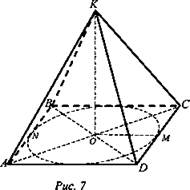
Решение: По определению ОМ - средняя линия ΔACD, поэтому AD = 2ОМ, AD = 2lcosα.

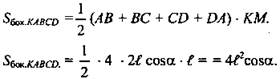
(Ответ: 4l2cosα.)

Карточка 5

Дано: В шар вписана правильная шестиугольная усеченная пирамида О ∈ (АВС); АО = ОА1 = R; ∠А1АО = α (рис. 8).

Найти: Vпирам.

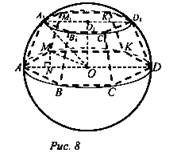
Решение: Так как радиус описанной окружности около правильного шестиугольника равен стороне (АО = ОМ = AM = R), то ∠MAN = 60°. В ΔAMN: ∠AMN = 30°, следовательно, AN = R/2, тогда по теореме Пифагора

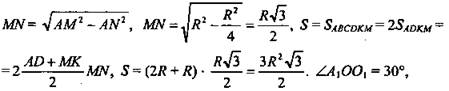
Тогда A1O1 = R/2. Аналогично найдем Из ΔA1OO1 пo теореме Пифагора Найдем

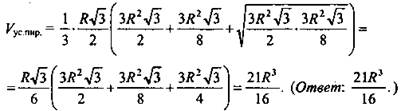
Карточка 6

Дано: в шар вписан конус, SABC = S, ∠ABO = α (рис. 9).

Найти: Vшара.

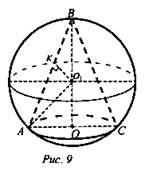
Решение: Из ΔАО1КВ по определению косинуса угла

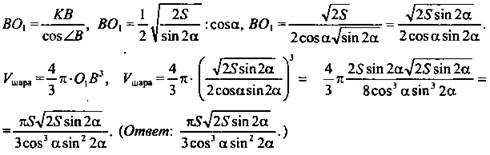
IV. Самостоятельное решение задач

Задача № 757 (рис. 10).

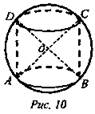
Решение: из ΔOCB по теореме косинусов Применяя формулу половинного угла и извлекая арифметический квадратный корень, получим CО = R, где R - радиус шара. Тогда (Ответ: .

Наводящие вопросы:

- почему cos(180° - α) = -cosa?

- почему СО = ОВ?

- почему извлекали арифметический квадратный корень?

Задача № 759 (рис. 11).

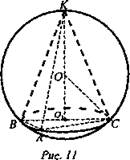
Решение: ОВ1 = O1С = 1 (см). Из ΔКО1С по определению тангенса угла KO1 = tgα. Пусть КО = R, тогда OO1 = КО1 - КО, OO1 = tgα - R. Из ΔOCO1 по теореме Пифагора

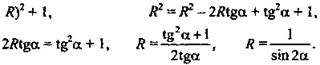
Sсферы (Ответ: ).

Задача № 760 (рис. 12).

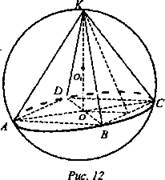
Решение: Из ΔКО1С по определению тангенса угла Пусть КО = R, тогда OO1 = KO1 - KО. OO1 = 5tgβ - R. Из ΔОО1С по теореме Пифагор.

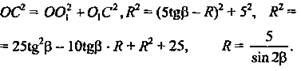
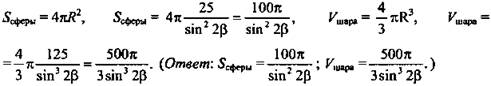
Дополнительная задача

Около правильной треугольной призмы, высота которой вдвое больше стороны ее основания, описан шар. Найдите отношение объема шара к объему призмы.

Дано: около призмы описан шар, АВ = ВС = АС, ВВ1 = 2АВ (рис. 13).

Найти:

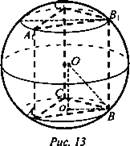
Решение: пусть АВ = а, тогда BB1 = 2АВ; ВВ1 = 2а. Найдем О1В - радиус описанной окружности около ΔАВС (равносторонний), поэтому Из ΔОО1В по теореме Пифагора (Ответ: )

V. Подведение итогов

Домашнее задание

Задачи № 748, 749.

Дополнительная задача.

В шар радиуса 6 см вписан цилиндр. Найдите объем цилиндра, если плоскости его основания делят поверхность шара на три равные по площади части (рис. 14).

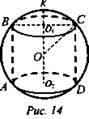
Решение: Из ΔОО1С по теореме Пифагор.

(Ответ: )