Высшая математика мини-справочник для ВУЗов
Правило Лопиталя - ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Теорема. Если функции f(х) и g(x) непрерывны в точке а и b некоторой ее окрестности, имеют производные в окрестности точки а, причем ![]() и существует
и существует ![]() то существует предел отношения функций f(х) и
то существует предел отношения функций f(х) и ![]() и справедливо равенство
и справедливо равенство
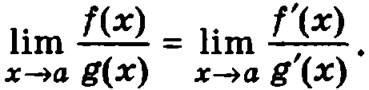
Пример. 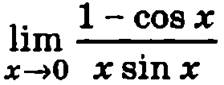
Числитель и знаменатель выражения, стоящего под знаком предела при х → 0, стремятся к нулю, и, следовательно, к данному пределу применимо правило Лопиталя:
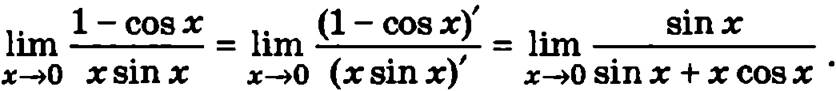
Полученное под знаком предела выражение опять представляет собой отношение двух бесконечно малых величин, к которому еще раз можно применить правило Лопиталя:

Теперь числитель выражения, стоящего под знаком предела, стремится к 1, а знаменатель — к 2 при х → 0.
Значит 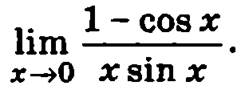
Данное правило будет справедливо и в том случае, когда ![]() то есть когда имеем дело с неопределенностью ∞/∞.
то есть когда имеем дело с неопределенностью ∞/∞.
Пример 
В данном случае имеем неопределенность ∞/∞, и к данному пределу можно применить правило Лопиталя:
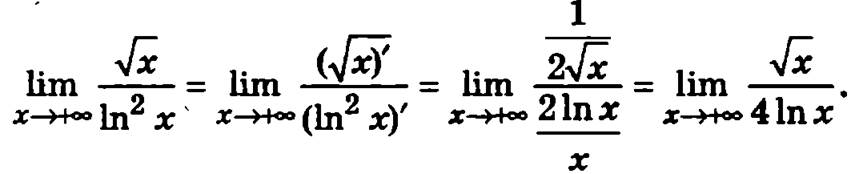
Опять имеем неопределенность ∞/∞, и еще раз применим правило Лопиталя:
