Высшая математика мини-справочник для ВУЗов
Приложение дифференциального исчисления к исследованию функций - ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Определение. Функция f(х) называется возрастающей на интервале (а, b), если для любых х1 и х2 из этого интервала, таких что х1 < х2, справедливо неравенство f(x1) ≤ f(x2).
Функция f(x) называется убывающей на интервале (а, b), если для любых х1 и х2 из этого интервала, таких, что х1 < х2, справедливо неравенство f(х1) ≥ f(x2).
Теорема. Для того чтобы функция f(x), имеющая производную, возрастала на интервале (а, b), необходимо и достаточно, чтобы всюду на этом интервале выполнялось неравенство f'(x) ≥0. А для того чтобы функция f(x), имеющая производную, убывала на том же интервале, необходимо и достаточно, чтобы всюду на (а, b) выполнялось неравенство f'(x) ≤ 0.
Теорема. Если при переходе через точку x0, в которой f'(x0) = 0, знак производной f’(x) меняется с «минуса» на «плюс», то в точке х0 функция f(х) имеет минимум, если, знак меняется с «плюса» на «минус», то в точке х0 функция f(x) имеет максимум. Если при переходе через точку знак производной не меняется, то в этой точке функция f(x) не имеет экстремума.
Пример. Рассмотрим функцию 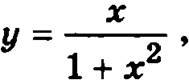 которая определена на всей действительной оси, и найдем ее интервалы возрастания и убывания, а также экстремумы. Для этого вычислим ее первую производную:
которая определена на всей действительной оси, и найдем ее интервалы возрастания и убывания, а также экстремумы. Для этого вычислим ее первую производную:
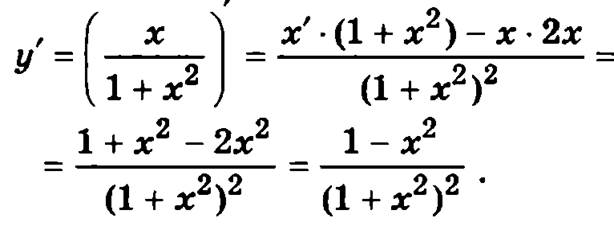
Далее найдем нули числителя и знаменателя производной 1 — х2 = 0, x2 = 1, x1 = -1, х2 = 1.
Так как 1 + х2 ≠ 0, знаменатель в нуль не обращается.
Отметим найденные нули на числовой оси:

В результате числовая ось разобьется на три интервала (-∞, -1), (-1, 1) и (1, +∞). На каждом интервале производная функции у’ будет сохранять знак (то есть будет во всех точках интервала или положительной или отрицательной). Для того чтобы определить знак производной на интервале, надо вычислить ее значение в какой-либо точке этого интервала. Так, например, в точке х = -2, принадлежащей интервалу (-∞, -1), значение производной 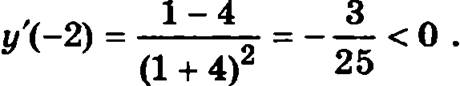 Значит, на всем интервале (-∞, -1) производная отрицательна и функция на нем убывает.
Значит, на всем интервале (-∞, -1) производная отрицательна и функция на нем убывает.
Аналогично, вычислив у'(0) = 1 > 0 и учитывая, что точка х = 0 принадлежит интервалу (-1, 1), можно сделать вывод, что производная на интервале (-1, 1) положительна и функция на нем возрастает.
Вычислив значение производной у'(3) = -8/100 < 0, делаем вывод, что на интервале (1, +∞), которому принадлежит точка х = 3, производная функции отрицательна и функция убывает.
Так как производная функции при переходе через точку х = -1 меняет знак с «минуса» на «плюс», в этой точке функция имеет минимум. Для того чтобы найти этот минимум следует подставить значение х = -2 в функцию ymin = y(-1) = -1/2.
При переходе через точку производная меняет знак с «плюса» на «минус» и значит в точке х = 1 функция имеет максимум, равный ymax = y(1) = 1/2.
Определение. Говорят, что функция f(x) на интервале (а, b) выпукла, если касательная, проведенная в каждой точке этого интервала, располагается выше графика функции. Говорят, что функция f(x) на интервале (а, b) вогнута, если касательная, проведенная в каждой точке этого интервала, располагается ниже графика функции.
Теорема. Если функция f(x) на интервале (а, b) выпукла и имеет в каждой точке данного интервала вторую производную, то вторая производная на всем интервале (а, b) неположительнаf''(x) ≤ 0. Если функция (а, b) на интервале (а, b) вогнута и имеет в каждой точке данного интервала вторую производную, то вторая производная на всем интервале (а, b) неотрицательна.f''(x) ≤ 0.
Теорема. Если в каждой точке интервала (а, b) функция f(x) имеет отрицательную вторую производную f''(x) < 0, то на указанном интервале функция f(x) выпукла. Если в каждой точке интервала (а, b) функция f(х) имеет положительную вторую производную f''(x) > 0, то на указанном интервале функция f(x) вогнута.
Определение. Точкой перегиба функции f(х) называется точка, которая отделяет интервал выпуклости функции f(x) от интервала вогнутости.
Теорема. Если при переходе через точку х0 вторая производная функции f''(x) меняет знак, то эта точка является точкой перегиба функции f(x).
Пример. Определим интервалы выпуклости и вогнутости функции 
Найдем вторую производную функции ![]() и определим ее нули
и определим ее нули 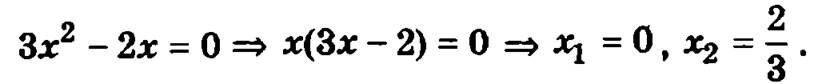
Отметим нули функции на числовой оси:
Вся числовая ось оказалась разделенной на три интервала (-∞, 0), (0, 2/3) и (2/3, +∞). На каждом из полученных интервалов вторая производная функции у’’ будет сохранять знак. Определим знак второй производной функции так, как это было сделано в предыдущем примере.
у''(-1) = 5, и значит на всем интервале (-∞, 0), в котором расположена точка х = -1, вторая производная функции будут положительна, а сама функция будет вогнутой. у’’(1/2) = -1/4, и на интервале (0, 2/3), которому принадлежит точка х = 1/2, вторая производная будет отрицательной, а функция — выпуклой. у’’(1) = 1 на интервале (2/3, +∞) вторая производная положительна, а функция вогнута.
Попутно были определены и точки перегиба, отделяющие интервалы вогнутости от интервалов выпуклости. Это точки х = 0 и х = 2/3.