Асимптоты - ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Определение. Асимптотой графика функции у = f(x) называется такая прямая у = kx + b, для которой разность f(х) - kx - b стремится к нулю при х → ∞.

Асимптоты бывают вертикальными и невертикальными.

Если в точке х = х0 функция у = f(x) терпит разрыв второго рода (то есть если в этой точке равен бесконечности хотя бы один из односторонних пределов то вертикальная прямая х = х0 является вертикальной асимптотой графика функции.

Для определения невертикальных асимптот вычисляются пределы

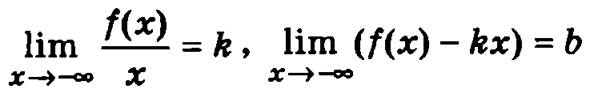
и

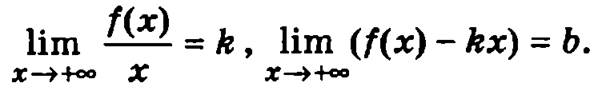
Если существуют и конечны первые два предела, то говорят, что существует левосторонняя асимптота и значения этих пределов определяют ее параметры k и b.

Если существуют и конечны вторые два из приведенных выше пределов, то говорят что существует правосторонняя асимптота и значения этих пределов определяют ее параметры k и b.

Иногда левосторонняя и правосторонняя асимптоты совпадают, такая асимптота называется двухсторонней.

Пример. Найдем асимптоты графика функции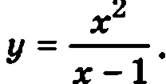

В точке х = 1 функция неопределенна и ее односторонние пределы в этой точке равны Следовательно в этой точке функция имеет разрыв второго рода, а уравнение ее вертикальной асимптоты х = 1.

Найдем невертикальные асимптоты графика функции:

Так как вычислялись пределы при х → ±∞, то найденные параметры определяют двухстороннюю асимптоту у = х + 1. Схематически расположение асимптот, изображенных пунктирными линиями, и графика функции представлено на рис. 8.

Рис. 8