Путешествие в историю математики - Свечников А. А. 1995
Как алгебра стала геометрической
Начертите квадрат со стороной в 1 см и подумайте, чему равна его площадь. Площадь такого квадрата будет равна 1 кв. см, так как 1 • 1 = 1 (см2). Начертите в этом квадрате отрезок, соединяющий вершины двух противоположных углов, — диагональ. Этот отрезок разделит квадрат на два равных треугольника. Один треугольник отличается от другого только положением.
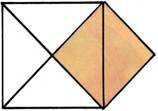
На проведенном отрезке — на диагонали — как на стороне постройте новый квадрат так, чтобы диагональ первого квадрата стала стороной нового квадрата. В новом квадрате соедините попарно вершины противоположных углов отрезками (т. е. проведите две диагонали). Второй квадрат окажется разделенным на четыре равных треугольника, а в первом квадрате равных им будет только два треугольника; следовательно, второй квадрат в два раза больше первого квадрата, т. е. его площадь равна 2 см2. А чему будет равна сторона второго квадрата? Обозначим ее через х. Чтобы вычислить площадь квадрата, надо его сторону (х) умножить на самое себя или х • х = 2 (см2).
Попытаемся подобрать такое число, которое при умножении на равное ему даст 2. Например, 1,5 • 1,5 = 2,25. Получили число больше двух. Следовательно, это число велико. Возьмем число меньше, чем 1,5, а именно 1,4. 1,4 • 1,4 = 1,96. Оказалось, что число 1,4 мало. Увеличим его: 1,41 • 1,41 = 1,9881. Полученное число опять меньше 2. Испытаем большее число 1,42. Получим 1,42 • 1,42 = 2,0164. Следовательно, х < 1,42. Мы нашли 1,41 <х< 1,42, т. е. в поиске значения х мы приблизились к его значению, но точного выражения для него не нашли.
Если продолжить поиск числа х, то можно еще ближе подойти к истинному значению х, но точного значения числа, которое, будучи умноженным само на себя, дало бы в произведении 2, мы никогда не найдем. Евклид доказал, что таких дробных чисел нет.
Измерить диагональ квадрата, сторона которого равна 1, и выразить результат точным числом нельзя. Поэтому сторону квадрата и его диагональ назвали несоизмеримыми. Свойство несоизмеримости стороны и диагонали квадрата было открыто пифагорийцами.
Пифагор и его последователи анализировали свойства натуральных чисел. Среди них они выделяли четные и нечетные, треугольные и квадратные, дружные, избыточные и ряд других. Однако дроби они к числам не относили. Пифагорийцы считали их отношениями. Много внимания они уделяли изучению пропорций. Пифагорийцы пытались найти в природе и обществе постоянные вечные законы и свести все их к числовым соотношениям. Они полагали основой всего существующего числа и их отношения.
Пифагор открыл, что три колеблющиеся струны дают приятное для слуха гармоническое звучание, когда длины струн соотносятся как 3:4:6. Обнаружив ряд замечательных свойств чисел и числовых рядов, а также зависимость гармонии звуков от числовых соотношений, пифагорийцы приписали числам божественные свойства. Но когда было установлено существование несоизмеримых отрезков, когда математики не нашли числа, которыми можно было бы выразить отношение двух отрезков, пифагорийцы были обескуражены. Это открытие противоречило их утверждению: «Всё есть число». Они решили сохранить свое открытие о несоизмеримости отрезков в тайне.
Существует легенда о том, что один из пифагорийцев разгласил эту тайну и за это боги его страшно покарали — он погиб при кораблекрушении.
Научные открытия хранятся в тайне недолго. О несоизмеримости отрезков узнали и другие древнегреческие математики и стали искать способы преодоления создавшегося осложнения.
Греческий математик и астроном Евдокс (ок. 406 — 355 до н. э.) разработал теорию отношений и пропорций, в которой, чтобы избежать несоизмеримости, осознанно отверг числовые значения отрезков и рассматривал отношения только геометрических величин, т. е. отрезков и площадей. Этот подход позволил преодолеть затруднения, возникшие с открытием несоизмеримых отрезков.
Перейдя к изображению чисел отрезками, греческие математики стали рассматривать все арифметические операции как действия с отрезками и выполняли сложение, вычитание, умножение и деление посредством геометрических построений. Например, о произведении ab они говорили: «Прямоугольник, содержащийся между отрезками а и b», о выражении а2 = а • а: «Квадрат со стороной а» и т. д.
Так появилась алгебра, которая оперировала не числами и не буквами, а отрезками, площадями и объемами геометрических фигур. В дальнейшем преобразование назвали геометрической алгеброй. Она довольно долго способствовала прогрессу науки, так как давала возможность посредством геометрических построений с последующими доказательствами решать и исследовать разнообразные задачи из алгебры.
В «Началах» Евклида приведены доказательства алгебраических тождеств:
![]()
и др. Там же дано геометрическое решение уравнений вида ab = cx и более сложных.
Алгебра древних греков со времен Евклида превратилась в строгую математическую теорию. Хотя решения и доказательства посредством геометрических построений были очень громоздки и требовали много времени, все же геометрическая алгебра несколько веков способствовала развитию науки. В геометрических доказательствах алгебраических предложений греки достигли высокого искусства, но решения практических задач они избегали.
Совсем иначе подошел к изложению вопросов алгебры аль-Хорезми. Он показал, что алгебра может существовать самостоятельно, вне геометрии.